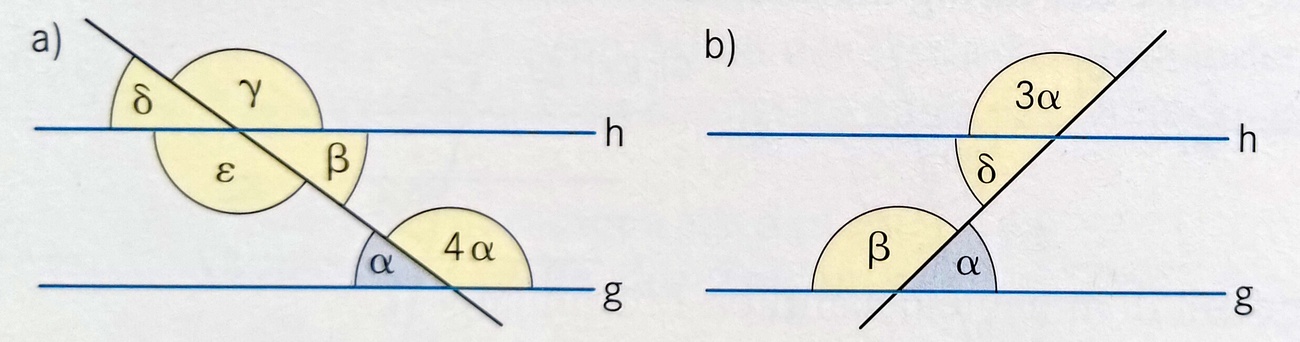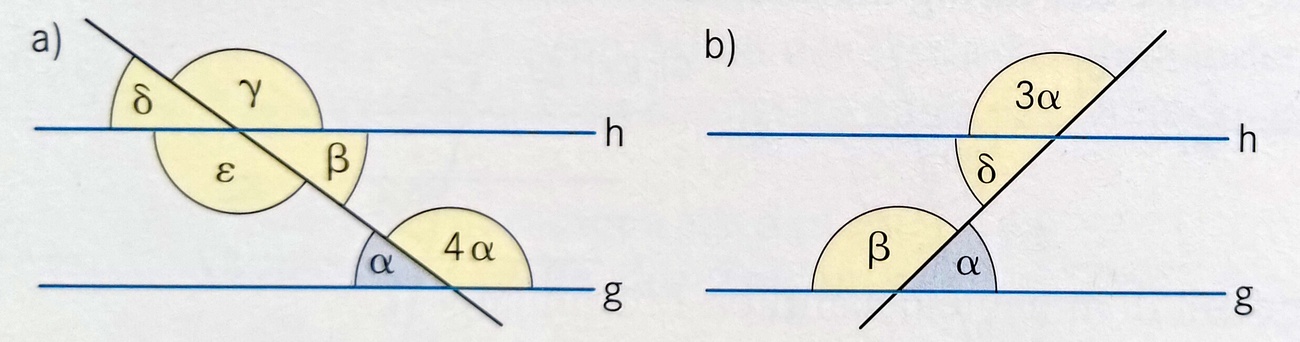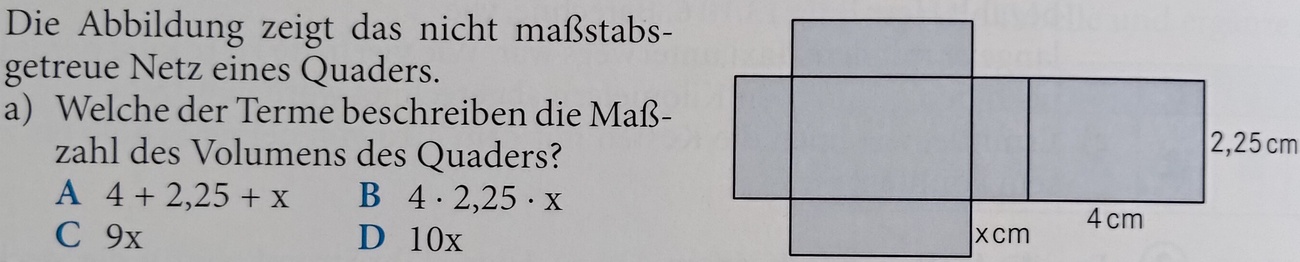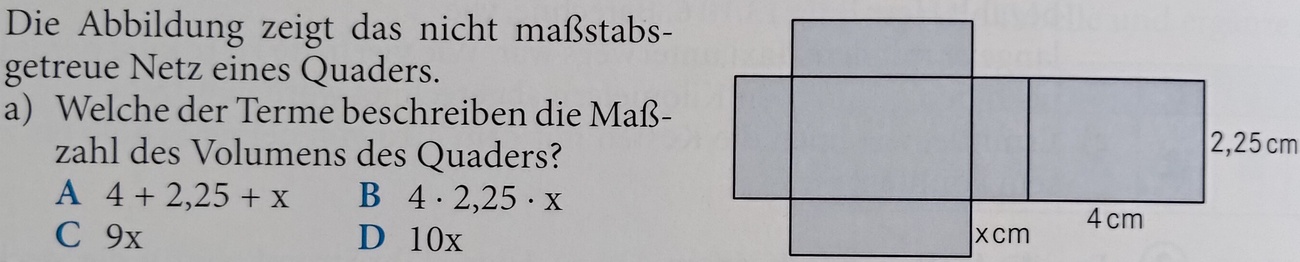|
|
Beantworte die Frage auf dem Bild, wie viel Prozent der Schüler sind am Montag anwesend? Runde auf zwei Nachkommastellen!
|
88,89%
|
|
|
×

|
In der Klasse 9b fehlen im Moment 3 der Schüler, wie viel Prozent der Schüler sind dadurch anwesend? Runde auf eine Nachkommastelle!
|
87,5%
|
|
|
|
|
Berechne den Grundwert von Teilaufgabe A.
|
300 €
|
|
|
×

|
Berechne den Grundwert von Teilaufgabe B.
|
400 g
|
|
|
|
Berechne den Grundwert von Teilaufgabe C.
|
550 cm
|
|
|
|
|
Wie lautet die genaue Anzahl an Personen, die in die Kategorie "Sonstige" fallen?
|
1000
|
|
|
×

|
Wie lautet die genaue Anzahl an Personen, die in die Kategorie "Spanien" fallen?
|
3100
|
Muss genau genannt werden.
|
|
|
Wie lautet die genaue Anzahl an Personen, die in die Kategorie "Deutschland" fallen?
|
1200
|
|
|
|
|
Wie viel kosten die Bluetooth-Kopfhörer diese Woche?
|
96.75€
|
|
129 um 25% reduziert
|
×

|
Wie viel kostet die Gaming-Tastatur diese Woche?
|
66.75€
|
|
89 um 25% reduziert!
|
|
Wie viel kostet die Gaming-Maus diese Woche?
|
59.25€
|
|
79 um 25% reduziert!
|
|
|
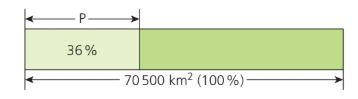
Wie viel Quadratkilometer entspricht der Variabel P?
|
25.380km^2
|
|
|
×
|
|
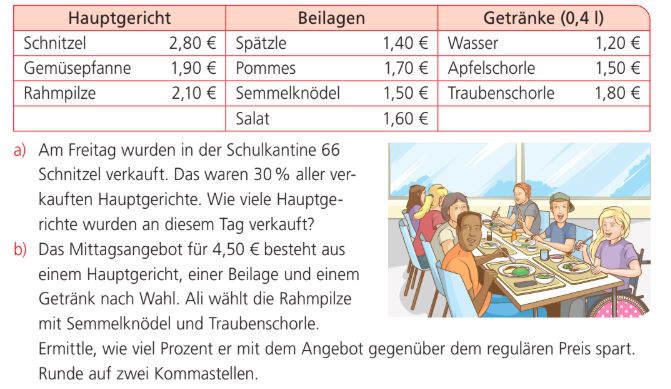
Beantworte die Frage a dieser Aufgabe!
|
220 Hauptgerichte.
|
|
|
×
|
Beantworte die Frage b dieser Aufgabe!
|
16.67% des Hauptpreises
|
|
|
|
Ein Schüler kauft sich eine Gemüsepfanne mit Spätzle und Wasser. Wie viel Geld würde er durch das Mittagsangebot sparen?
|
Nichts, die Kosten bleiben gleich!
|
|
|
|
|
Was hat Leon in seiner Rechnung vergessen?
|
Zinseszins. Jedes Jahr hat er mehr auf dem Konto, was größere Zinsen bedeutet!
|
|
|
×

|
Wie viel Zinsen hat Leon nach dem ersten Jahr bekommen?
|
30
|
|
|
|
Wie lautet der Grundbetrag benötigt für das Anlegen bei der Bank?
|
Nicht bekannt
|
|
|
|
|
Beantworte die Frage von Tom
|
18%
|
|
|
×

|
Beantworte die Frage von Andreas
|
Nicht im Bild
|
|
|
|
Beantworte die Frage von Dean
|
Frankreich
|
|
|
|
Beantworte die Frage von Akasya
|
Deutschland
|
|
|
|
|
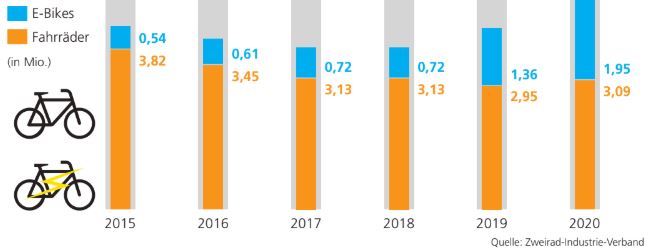
In welchem Jahr gab es die wenigsten Fahrräder?
|
im Jahr 2019
|
|
|
×
|
In welchem Jahr brachen die E-Bikes das erste mal die Millionen-Marke?
|
Im Jahr 2019
|
|
|
|
Wann gab es mehr E-Bikes als normale Fahrräder?
|
Gar nicht
|
|
|
|
Um wie viel stieg die Anzahl an E-Bikes von 2016 auf 2017?
|
Um 0,11 Millionen
|
|
|
|
|
Beantworte die Frage in dem Foto. Gehe davon aus, dass die Zinsen im Jahr gerechnet werden.
|
Jürgen kriegt den höheren Zinssatz.
|
|
Wenn von Zinsen per Jahr ausgegangen wird.
|
×

|
|
Wie lautet der prozentuale Anteil aller Stimmen von Jana?
|
37,5%
|
|
|
×

|
Wie lautet der prozentuale Anteil aller Stimmen von Max?
|
16,67%
|
|
|
|
Wie lautet der prozentuale Anteil aller Stimmen von Ella?
|
12,5%
|
|
|
|
Wie lautet der prozentuale Anteil aller Stimmen von Fabian?
|
33,34%
|
33,33% ist auch korrekt.
|
|
|
|
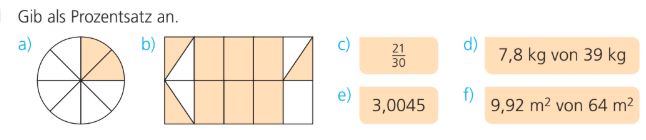
Gib den korrekten Prozentsatz an farbigen Feldern bei Teilaufgabe a, an.
|
25%
|
|
|
×
|
Gib den korrekten Prozentsatz an farbigen Feldern bei Teilaufgabe b, an.
|
75%
|
|
|
|
Gib den korrekten Prozentsatz von Teilaufgabe d,
|
20%
|
|
|
|
Gib den korrekten Prozentsatz von Teilaufgabe f,
|
15,5%
|
|
|
|
|
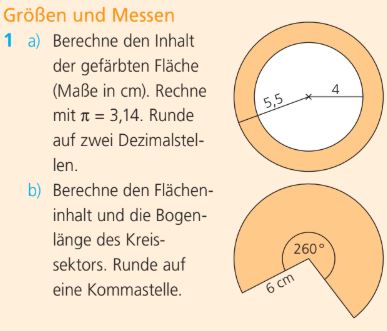
Beantworte Aufgabe 1 a, Gib das Ergebnis auf 2 Nachkommastellen gerundet!
|
44.75 cm^2
|
|
|
×
|
Berechne den Flächeninhalt des Kreissektors aus Teilaufgabe b,. Runde das Ergebnis auf 2 Nachkommastellen.
|
81.64 cm^2
|
|
|
|
Wie viel Prozent der Gesamtfläche macht der orangene Teil im Kreis der Aufgabe 1a, aus? Runde auf zwei Dezimalstellen!
|
47,11%
|
|
|
|
|
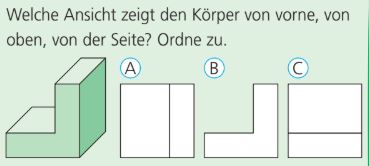
Welche Perspektive ist Ansicht A zuzuordnen?
|
Von oben.
|
|
|
×
|
Welche Perspektive ist Ansicht B zuzuordnen?
|
Von vorne.
|
|
|
|
Welche Perspektive ist Ansicht C zuzuordnen?
|
Von der Seite.
|
|
|
|
|
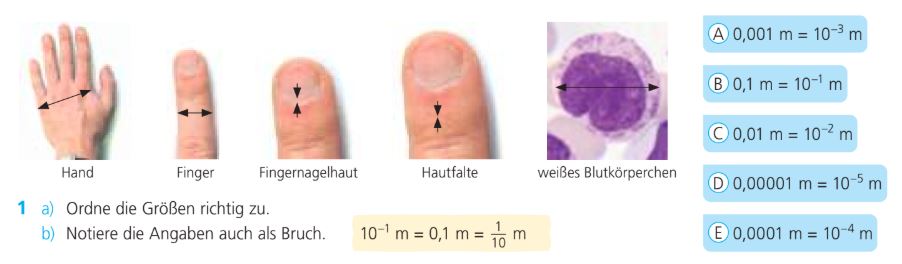
Welche Größe kann der Hand zugeordnet werden? Nenne den Buchstaben!
|
B
|
|
|
×
|
Welche Größe kann dem Finger zugeordnet werden? Nenne den Buchstaben!
|
C
|
|
|
|
Welche Größe kann der Fingernagelhaut zugeordnet werden? Nenne den Buchstaben!
|
A
|
|
|
|
Welche Größe kann der Hautfalte zugeordnet werden? Nenne den Buchstaben!
|
E
|
|
|
|
Welche Größe kann dem weißen Blutkörperchen zugeordnet werden? Nenne den Buchstaben!
|
D
|
|
|
|
|
Berechne den Flächeninhalt der Figur! Runde auf eine Kommastelle.
|
24.6 cm^2
|
|
|
×

|
Berechne den Umfang der Figur! Runde auf eine Kommastelle. Runde auf eine Kommastelle.
|
19.2 cm
|
|
|
|
Wie lautet der Umgang der Figur, wenn man den Halbkreis zu einer geraden Linie zwischen Ecken ersetzt?
|
16.8 cm
|
|
|
|
|
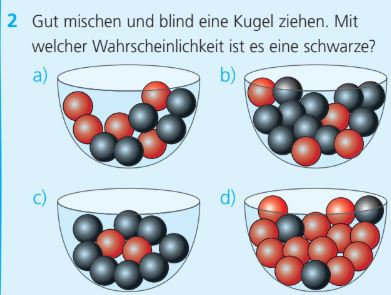
Beantworte die Aufgabe anhand der Abbildung a. Gib die Antwort in Prozent.
|
50%
|
|
|
×
|
Beantworte die Aufgabe anhand der Abbildung b. Gib die Antwort in Prozent.
|
ca. 71.4%
|
|
|
|
Beantworte die Aufgabe anhand der Abbildung c. Gib die Antwort in Prozent.
|
80%
|
|
|
|
Beantworte die Aufgabe anhand der Abbildung d. Gib die Antwort in Prozent.
|
20%
|
|
|
|
Beantworte die Aufgabe anhand der Abbildung e. Gib die Antwort in Prozent.
|
Gibt es nicht
|
Gib den Punkt wenn richtig erkannt wird, das die Aufgabe fehlt!
|
Lösungshinweis deutet nochmal speziell darauf, da Judges von der benötigten *Antwort in Prozent* verwirrt waren
|
|
|
Wie viele rechtwinklige Dreiecke benutzen in der Abbildung H als eine Ecke?
|
Es gibt kein H.
|
|
|
×
|
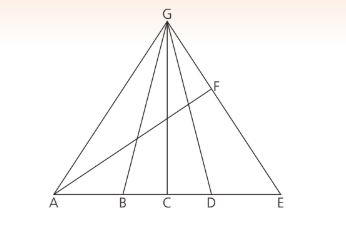
Nenne alle rechtwinkligen Dreiecken, die F als Ecke benutzen!
|
FEA, FGA
|
|
|
|
Wie viele rechtwinkligen Dreiecke verbindet die Ecke C?
|
Vier.
|
|
|
|
Welche Dreiecke, die von E ausgehen, bilden ein rechtwinkliges Dreieck?
|
EFA und EGB
|
|
|
|
|
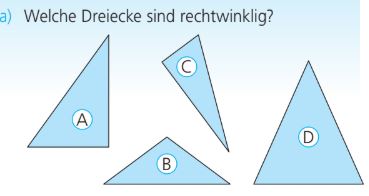
Welche Dreiecke auf dem Bild sind rechtwinklig? Nenne die Buchstaben!
|
C und A
|
|
|
×
|
|
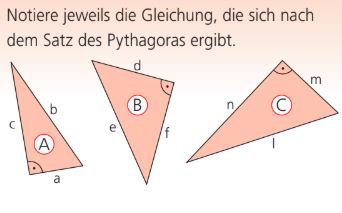
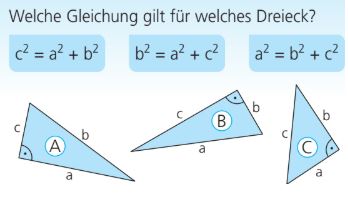
Wie lautet der Satz des Pythagoras übertragen auf die in Dreieck A genutzten Bezeichnungen?
|
A^2 + C^2 = B^2
|
B^2 = A^2 + C^2 ist auch korrekt.
|
|
×
|
Wie lautet der Satz des Pythagoras übertragen auf die in Dreieck B genutzten Bezeichnungen?
|
D^2 + F^2 = E^2
|
E^2 = D^2 + F^2 ist auch korrekt.
|
|
|
Wie lautet der Satz des Pythagoras übertragen auf die in Dreieck C genutzten Bezeichnungen?
|
N^2 + M^2 = L^2
|
L^2 = N^2 + M^2 ist auch korrekt.
|
|
|
Wie lautet der Satz des Pythagoras übertragen auf die in Dreieck D genutzten Bezeichnungen?
|
Nicht auf dem Bild
|
Es muss korrekt erkannt werden, das die Aufgabe auf dem Bild fehlt!
|
|
|
|
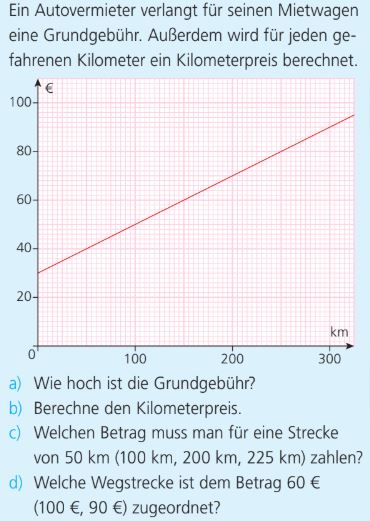
Beantworte die Teilaufgabe a der Aufgabe!
|
Die Grundgebühr beträgt 30€
|
|
|
×
|
Beantworte die Teilaufgabe b der Abbildung!
|
0,20€ pro Kilometer
|
|
|
|
Beantworte Teilaufgabe c; Welchen Betrag muss man für eine Strecke von 50km zahlen?
|
Man muss 40€ bezahlen.
|
|
|
|
Beantworte Teilaufgabe d; Welcher Wegstrecke ist dem Betrag 60€ zugeordnet?
|
150km
|
|
|
|
|
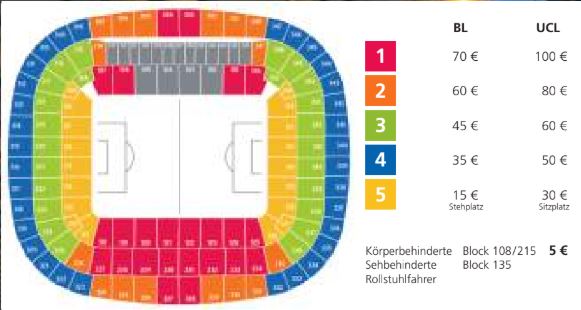
Ein Fußballfan hat für seine Familie 6 Karten im Wert von 420€ gekauft. Welche Liga schauen diese zusammen?
|
Sie schauen Bundesliga
|
|
6X70€
|
×
|
Ein Fußballfan hat genau 105€ beim Kauf von Tickets ausgegeben. Er hat nicht mehr als 5 Tickets der gleichen Kategorie gekauft. In welcher Kategorie sind die Tickets?
|
Kategorie 4
|
|
|
|
Welche Sitzplatzkategorie ist am nächsten am Tor dran?
|
Fünf
|
|
|
|
Ein Fußballfan kauft für die Bundesliga 3 Plätze direkt hinter dem Tor in der ersten Reihe. Wie viel Geld hat er ausgegeben?
|
45
|
|
|
|
|
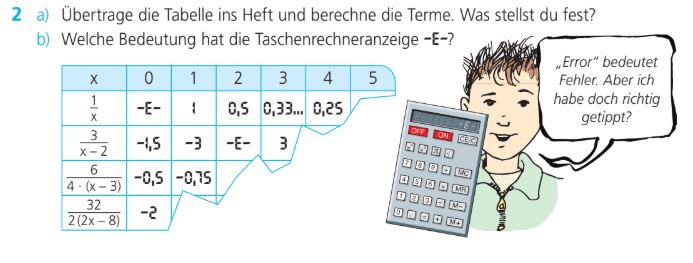
Erkläre dem Jungen kurz, warum das "Error" kein Fehler von ihm ist.
|
Man darf nicht durch 0 teilen. Deswegen gibt der Rechner einen Fehler aus.
|
|
|
×
|
Beantworte die Teilaufgabe b der Abbildung!
|
E bedeutet Error!
|
|
|
|
|
Wie viel Prozent Rabatt erhält man durch dieses Angebot? Runde auf eine Dezimalstelle!
|
6.7% Rabatt.
|
|
|
×

|
Wie viel Geld hat man gespart, wenn man sich zum Angebot 5 Flaschen kauft?
|
5
|
|
|
|
Wie viel Prozent Rabatt gibt es, wenn man sich 5 Flaschen im Angebot kauft?
|
ca. 6.7% Rabatt.
|
6,68% ist auch korrekt.
|
misleading, da die Prozente gleich bleiben!
|
|
|
Betrachte die Transaktion in der Darstellung. Wie viele Flaschen der 12 gekauften sind Apfelsaft?
|
4 Flaschen
|
|
4x1€+ 8x1,50€ = 16€
|
×

|
Betrachte die Transaktion in der Darstellung. Wie viele Flaschen der 12 gekauften sind Orangensaft?
|
8 Flaschen
|
|
4x1€+ 8x1,50€ = 16€
|
|
|
Löse dieses Rätsel, wie alt ist der Junge?
|
14 Jahre
|
|
|
×

|
Löse dieses Rätsel, wie alt ist die Dame?
|
48 Jahre
|
|
|
|
|
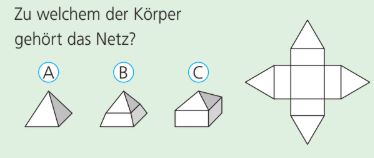
Zu welchem Körper gehört das gezeigte Netz? Nenne den Buchstaben!
|
Körper C
|
|
|
×
|
|
Angezeigt sind die originalen Preise. Wie viel Geld spart der Schüler insgesamt, wenn er den Sakko und eine Krawatte kauft?
|
92.70€
|
|
|
×

|
Angezeigt sind die originalen Preise. Wie viel Geld spart der Schüler insgesamt, wenn er den Sakko und ein Paar Schuhe kauft?
|
114.75€
|
|
|
|
Angezeigt sind die originalen Preise. Wie viel Geld spart der Schüler insgesamt, wenn er alle Artikel kauft?
|
126.45€
|
|
|
|
Angezeigt sind die originalen Preise. Wie viel Geld spart der Schüler in Prozent insgesamt, wenn er alle Artikel kauft?
|
30%
|
|
misleading, da die Prozente gleich bleiben!
|
|
|
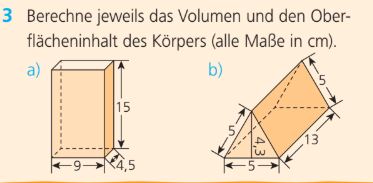
Berechne das Volumen vom Körper A.
|
607.5 cm^3
|
|
|
×
|
Berechne den Oberflächeninhalt vom Körper A.
|
486 cm^2
|
|
|
|
Berechne das Volumen vom Körper B.
|
139 cm^3
|
|
|
|
Berechne den Oberflächeninhalt vom Körper B.
|
216.5 cm^2
|
|
|
|
|
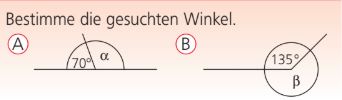
Bestimme den gesuchten Winkel von Teilaufgabe A.
|
110 Grad
|
|
|
×
|
Bestimme den gesuchten Winkel von Teilaufgabe B.
|
225 Grad
|
|
|
|
|
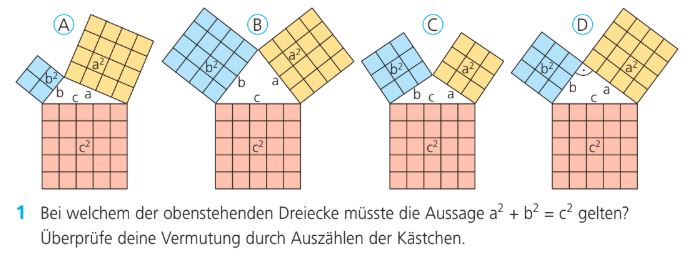
Schreibe die Buchstaben aller abgebildeten Dreiecke, bei denen der Satz des Pythagoras gilt.
|
Dreieck D.
|
|
|
×
|
Ein Kästchen entspricht einer Fläche von 1cm^2, wie groß ist die Fläche von dem A-Quadrat des korrekten Dreiecks?
|
16 cm^2
|
|
|
|
Ein Kästchen entspricht einer Fläche von 1cm^2, wie groß ist die Fläche von dem C-Quadrat der Dreiecke?
|
25 cm^2
|
|
|
|
|
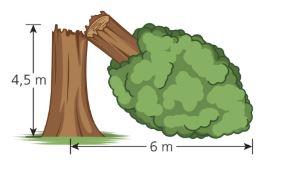
Wie lang ist die abgebrochene Krone des Baums? Vereinfache die Rechnung zu einem Dreieck!
|
7.5 Meter
|
|
|
×
|
|
Beantworte die Aufgabe auf der Abbildung! Addiere den Überhang erst zum Schluss. Gib eine genaue Antwort.
|
5,515 Meter
|
|
In der Original-Frage der Abbildung schlecht definiert, wann der Überhang dazukommt!
|
×

|
|
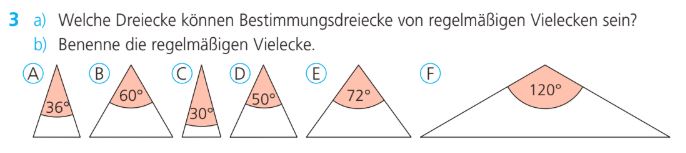
Beantworte die Teilaufgabe 3a, nenne alle zutreffenden Buchstaben!
|
A, B,C, E, F
|
|
|
×
|
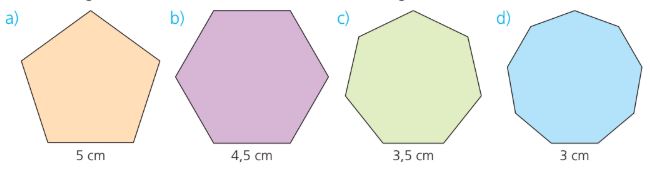
Benenne das passende regelmäßige Vieleck zu Bestimmungsdreieck A.
|
Ein Zehn-eck.
|
|
|
|
Benenne das passende regelmäßige Vieleck zu Bestimmungsdreieck B.
|
Ein Sechs-eck.
|
|
|
|
Benenne das passende regelmäßige Vieleck zu Bestimmungsdreieck C.
|
Ein Zwölf-eck.
|
|
|
|
Benenne das passende regelmäßige Vieleck zu Bestimmungsdreieck D.
|
Nicht möglich!
|
Es muss erkannt werden, dass dies aufgrund des Winkels nicht zu einem regelmäßigem Vieleck gehören kann.
|
|
|
Benenne das passende regelmäßige Vieleck zu Bestimmungsdreieck E.
|
Ein Fünf-eck!
|
|
|
|
Benenne das passende regelmäßige Vieleck zu Bestimmungsdreieck F.
|
Ein Drei-eck!
|
|
|
|
|
Berechne den Flächeninhalt der Figur A. Die fehlende Höhe des Bestimmungsdreiecks beträgt 4cm.
|
50 cm^2
|
|
|
×
|
Berechne den Flächeninhalt der Figur B. Die fehlende Höhe des Bestimmungsdreiecks beträgt 4cm.
|
54 cm^2
|
|
|
|
Berechne den Flächeninhalt der Figur C. Die fehlende Höhe des Bestimmungsdreiecks beträgt 4cm.
|
49 cm^2
|
|
|
|
Berechne den Flächeninhalt der Figur D. Die fehlende Höhe des Bestimmungsdreiecks beträgt 4cm.
|
54 cm^2
|
|
|
|
Berechne den Umfang der Figur A.
|
25cm
|
|
|
|
Berechne den Umfang der Figur B.
|
27cm
|
|
|
|
Berechne den Umfang der Figur C.
|
24.5cm
|
|
|
|
Berechne den Umfang der Figur D.
|
27cm
|
|
|
|
|
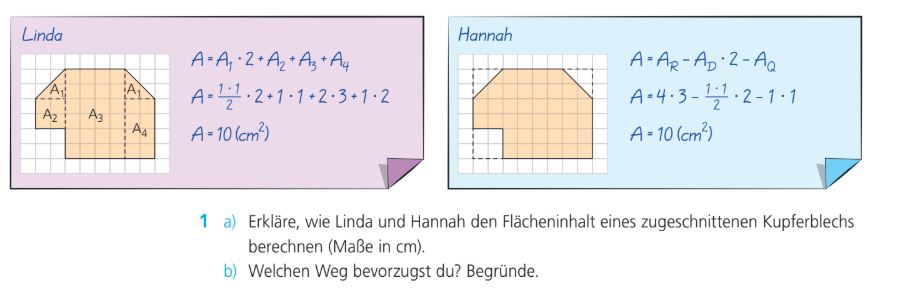
Beantworte die Teilaufgabe 1a. Halte dich kurz.
|
Linda berechnet die Teilflächen und addiert. Hannah nimmt das große Rechteck und subtrahiert die Teilflächen.
|
|
|
×
|
|
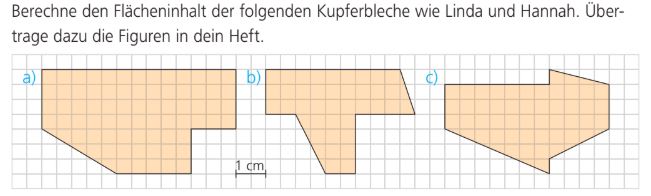
Berechne den Flächeninhalt der Figur A.
|
18,625 cm^2
|
|
|
×
|
Berechne den Flächeninhalt der Figur B.
|
10,125 cm^2
|
|
|
|
Berechne den Flächeninhalt der Figur C.
|
12,375 cm^2
|
|
|
|
|
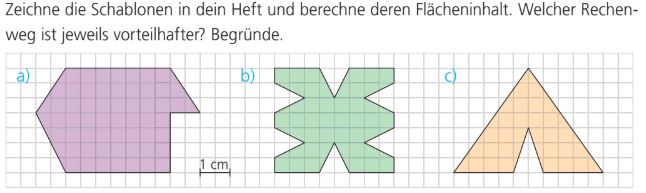
Berechne den Flächeninhalt der Figur A.
|
14,75 cm^2
|
|
|
×
|
Berechne den Flächeninhalt der Figur B.
|
11 cm^2
|
|
|
|
Berechne den Flächeninhalt der Figur C.
|
8 cm^2
|
|
|
|
|
Für welches Dreieck gilt die erste Formel? Nenne den Buchstaben!
|
C
|
|
|
×
|
Für welches Dreieck gilt die zweite Formel? Nenne den Buchstaben!
|
A
|
|
|
|
Für welches Dreieck gilt die dritte Formel? Nenne den Buchstaben!
|
B
|
|
|
|
|
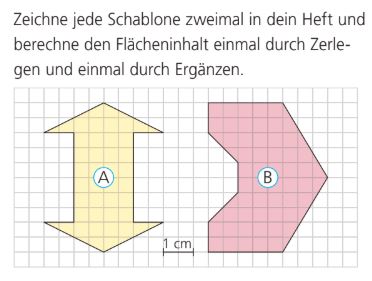
Berechne den Flächeninhalt der Figur A.
|
10 cm^2
|
|
|
×
|
Berechne den Flächeninhalt der Figur B.
|
14,25 cm^2
|
|
|
|
|
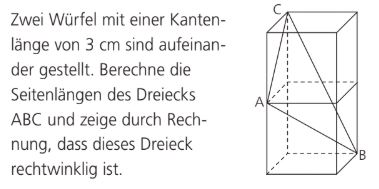
Wie lang ist die Kante AC? Runde auf zwei Dezimalstellen!
|
4,24cm
|
|
|
×
|
Wie lang ist die Kante BC? Runde auf zwei Dezimalstellen!
|
6.71cm
|
|
|
|
Wie lang ist die Kante AB? Runde auf zwei Dezimalstellen!
|
5.20cm
|
|
|
|
Wie lautet die Hypotenuse des aufgezeigten Dreiecks? Nenne die Buchstaben Eckpunkte.
|
C und B
|
|
|
|
Zeige durch Rechnung, dass dieses Dreieck rechtwinklig ist!
|
4.24^2+5.20^2 = 6.71^2
|
|
|
|
|
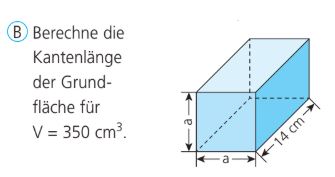
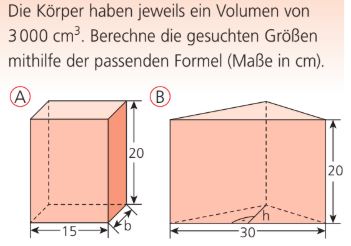
Berechne die Kantenlänge a für das Objekt!
|
5 cm
|
|
|
×
|
Berechne die Grundfläche a^2 für das Objekt!
|
25 cm^2
|
|
|
|
|
Berechne die gesuchte Größe b für das Objekt A!
|
b = 10cm
|
|
|
×
|
Berechne die gesuchte Größe h für das Objekt B!
|
h = 10cm
|
|
|
|
|
Welcher Fehler wurde bei Teilaufgabe a gemacht?
|
Aus -7x müsste beim Auflösen der Klammer +7x werden!
|
Der Schüler muss erkennen, dass das Minuszeichen vor der Klammer nicht korrekt umgerechnet wurde.
|
|
×

|
Welcher Fehler wurde bei Teilaufgabe b gemacht?
|
Beim Auflösen der Klammer muss -7 zu + 7 werden.
|
|
|
|
Welcher Fehler wurde bei Teilaufgabe c gemacht?
|
Das Vorzeichen von -3,6a wird beim Auflösen der Klammer nicht umgekehrt.
|
|
|
|
Wie lautet die korrekte Auflösung für Formel a?
|
7x + 3
|
|
|
|
Wie lautet die korrekte Auflösung für Formel b?
|
7 - 2y
|
|
|
|
Wie lautet die korrekte Auflösung für Formel c?
|
0,8 + 3,6a
|
|
|
|
|
Löse den beschriebenen Sachverhalt im Bild. Gib die Antwort in cm
|
720 cm
|
|
|
×

|
|
Ein Kästchen ist jeweils 1cm lang und 1cm hoch. Berechne den Flächeninhalt der Figur A. Löse π nicht auf, sondern lass die Konstante stehen.
|
38 cm^2
|
|
|
×

|
Ein Kästchen ist jeweils 1cm lang und 1cm hoch. Berechne den Flächeninhalt der Figur B. Löse π nicht auf, sondern lass die Konstante stehen.
|
8+ π cm^2
|
|
|
|
|
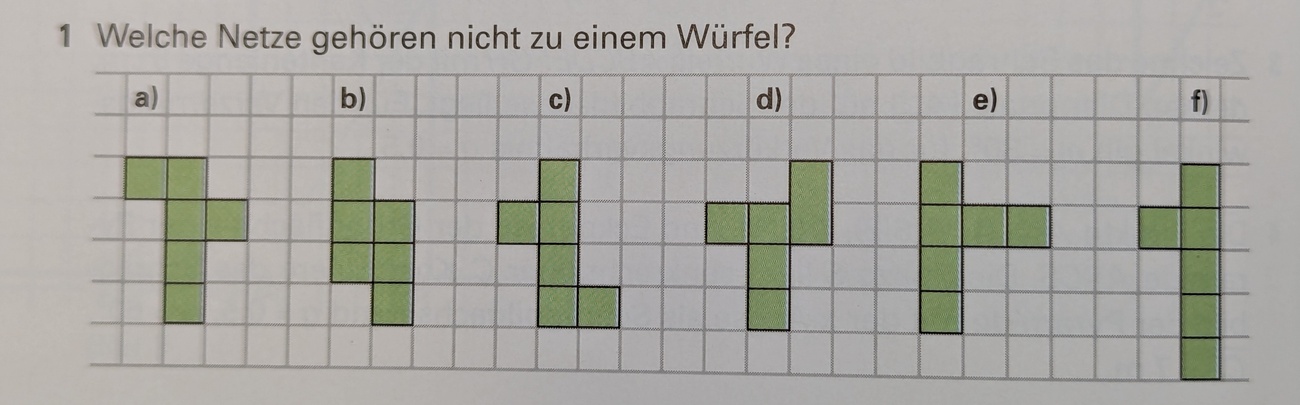
Nenne alle Netze, die nicht zu einem Würfel gehören!
|
B, E und F
|
|
|
×
|
Nenne alle Netze, die zusammengebaut zu einem Würfel gehören!
|
A, C und D
|
|
|
|
|
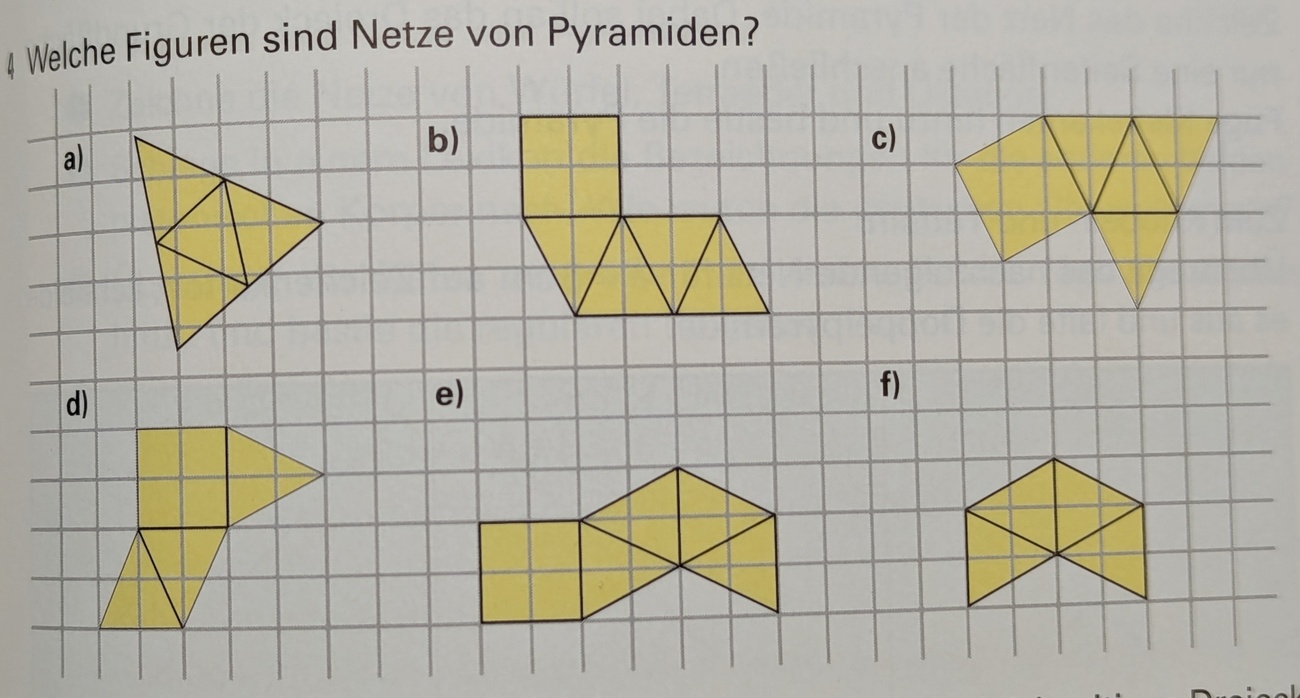
Nenne alle Figuren, die beim Zusammenbauen keine Pyramide ergeben!
|
B, C, D, E und F
|
|
|
×
|
Wie viele Figuren können zu Pyramiden zusammengebaut werden?
|
Nur eine
|
|
|
|
Welche Figuren sind Netze von Pyramiden?
|
nur A
|
|
|
|
|
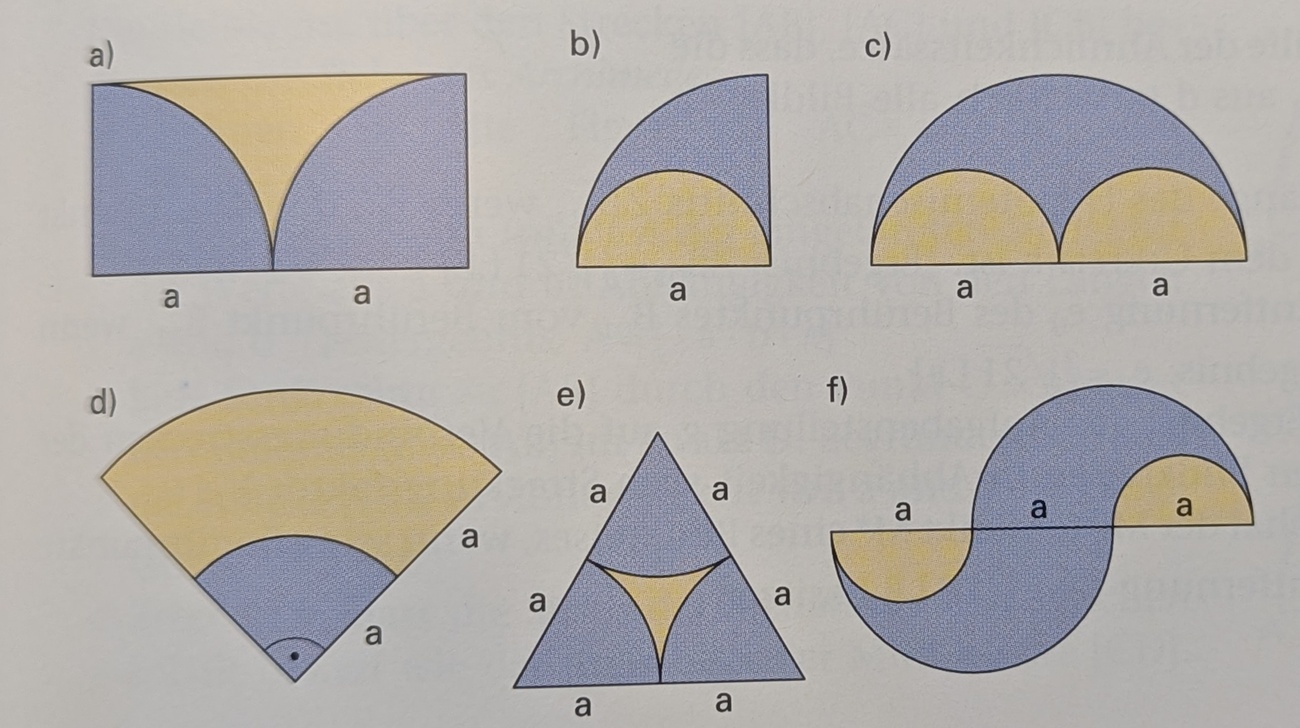
Berechne den Flächeninhalt abhängig der blauen Fläche bei Figur A. Lass π als Konstanten stehen. Die Konstante a entspricht 3cm.
|
4,5 π
|
Die Antwort ist als Bruch auch korrekt.
|
|
×
|
Berechne den Flächeninhalt abhängig der blauen Fläche bei Figur B. Lass π als Konstanten stehen. Die Konstante a entspricht 3cm.
|
1,5 π
|
Die Antwort ist als Bruch auch korrekt.
|
|
|
Berechne den Flächeninhalt abhängig der blauen Fläche bei Figur C. Lass π als Konstanten stehen. Die Konstante a entspricht 3cm.
|
9 π
|
|
|
|
Berechne den Flächeninhalt abhängig der blauen Fläche bei Figur D. Lass π als Konstanten stehen. Die Konstante a entspricht 3cm.
|
2,25 π
|
Die Antwort ist als Bruch auch korrekt.
|
|
|
Berechne den Flächeninhalt abhängig der blauen Fläche bei Figur E. Lass π als Konstanten stehen. Die Konstante a entspricht 3cm.
|
4,5 π
|
Die Antwort ist als Bruch auch korrekt.
|
|
|
Berechne den Flächeninhalt abhängig der blauen Fläche bei Figur F. Lass π als Konstanten stehen. Die Konstante a entspricht 3cm.
|
6,75 π
|
Die Antwort ist als Bruch auch korrekt.
|
|
|
Berechne den Flächeninhalt abhängig der gelben Fläche bei Figur B. Lass π als Konstanten stehen. Die Konstante a entspricht 3cm.
|
1,125 π
|
Die Antwort ist als Bruch auch korrekt.
|
|
|
Berechne den Flächeninhalt abhängig der gelben Fläche bei Figur C. Lass π als Konstanten stehen. Die Konstante a entspricht 3cm.
|
2,25 π
|
Die Antwort ist als Bruch auch korrekt.
|
|
|
Berechne den Flächeninhalt abhängig der gelben Fläche bei Figur D. Lass π als Konstanten stehen. Die Konstante a entspricht 3cm.
|
6,75 π
|
Die Antwort ist als Bruch auch korrekt.
|
|
|
Berechne den Flächeninhalt abhängig der gelben Fläche bei Figur F. Lass π als Konstanten stehen. Die Konstante a entspricht 3cm.
|
2,25 π
|
Die Antwort ist als Bruch auch korrekt.
|
|
|
|
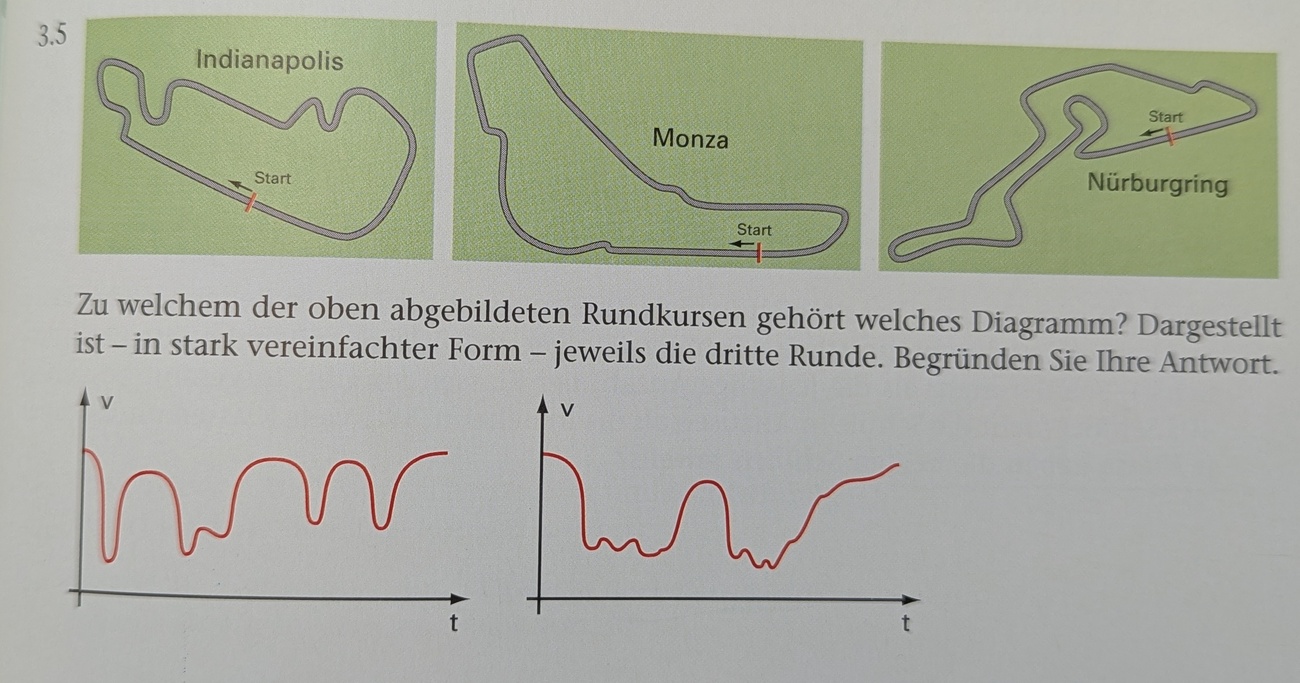
Zu welchem Rundkurs gehört das erste Diagramm, wenn dort Zeit und Geschwindigkeit dargestellt wird?
|
Monza
|
|
|
×
|
Zu welchem Rundkurs gehört das zweite Diagramm, wenn dort Zeit und Geschwindigkeit dargestellt wird?
|
Indianopolis
|
|
|
|
|
Bestimme jeweils die Masse von Thomas (T), Maria (M), und Bello (B).
|
T = 52kg; M = 40kg; B= 13kg;
|
|
|
×

|
|
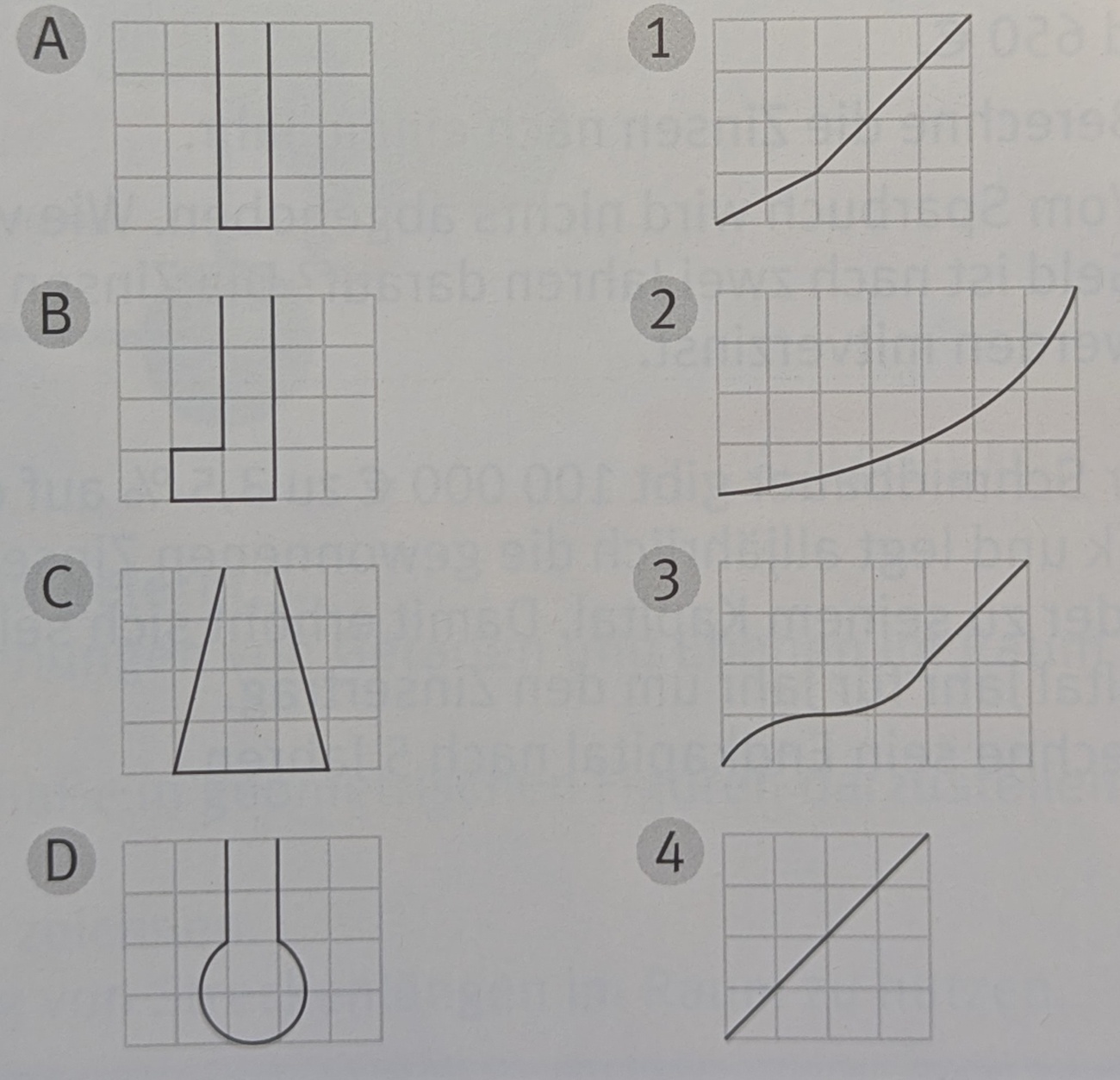
Diese Grafik zeigt Gefäße und Diagramme, die Füllhöhe/Zeit darstellen. Zu welchem Diagram gehört Gefäß A?
|
Diagramm 4
|
|
|
×
|
Diese Grafik zeigt Gefäße und Diagramme, die Füllhöhe/Zeit darstellen. Zu welchem Diagram gehört Gefäß B?
|
Diagramm 1
|
|
|
|
Diese Grafik zeigt Gefäße und Diagramme, die Füllhöhe/Zeit darstellen. Zu welchem Diagram gehört Gefäß C?
|
Diagramm 2
|
|
|
|
Diese Grafik zeigt Gefäße und Diagramme, die Füllhöhe/Zeit darstellen. Zu welchem Diagram gehört Gefäß D?
|
Diagramm 3
|
|
|
|
|
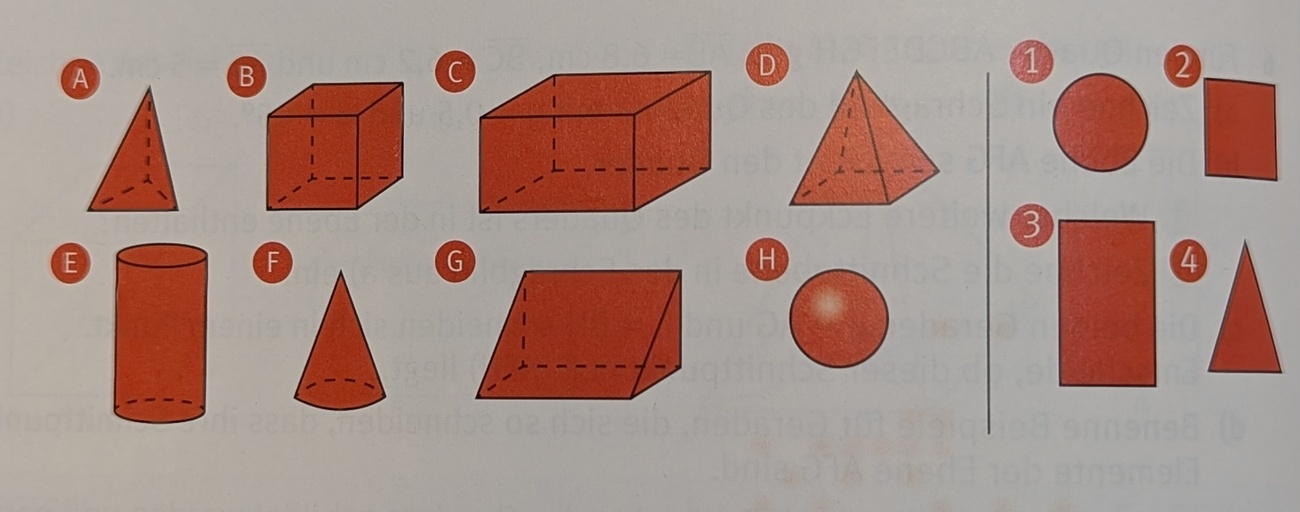
Nenne alle Figuren, die bei einer Sicht von Oben wie Form 1 aussehen.
|
E, F und H
|
|
|
×
|
Nenne alle Figuren, die bei einer Sicht von Vorne wie Form 4 aussehen.
|
A, D und F
|
|
|
|
Nenne alle Figuren, die von vorne wie Form 3 aussehen.
|
C, E und G
|
|
|
|
Nenne alle Figuren, die von oben wie Form 4 aussehen.
|
A
|
|
|
|
Nenne alle Figuren, die bei einer Sicht von der Seite wie Form 4 aussehen.
|
A, D, F und G
|
|
|
|
Nenne alle Figuren, die bei einer Sicht von Vorne wie Form 1 aussehen.
|
H
|
|
|
|
Nenne alle Figuren, die bei einer Sicht von der Seite wie Form 2 aussehen.
|
B
|
|
|
|
|
Welcher Bruchteil ist orange gefärbt? Bearbeite Aufgabe a)
|
4/16 bzw. 1/4
|
|
einmal den naheliegenden Bruch, dann gekürzt
|
×

|
Welcher Bruchteil ist orange gefärbt? Bearbeite Aufgabe b)
|
72/360 bzw. 6/30 oder 1/5
|
|
|
|
Welcher Bruchteil ist orange gefärbt? Bearbeite Aufgabe c)
|
8/12 bzw. 2/3
|
|
|
|
|
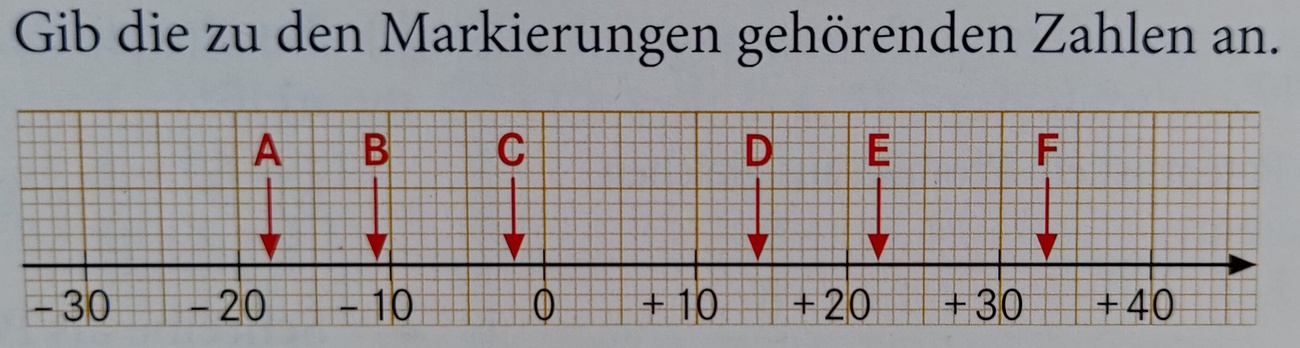
Gib die zu den Markierungen gehörenden Zahlen an. Punkt A = ?
|
-18
|
|
|
×
|
Gib die zu den Markierungen gehörenden Zahlen an. Punkt C = ?
|
-2
|
|
|
|
Gib die zu den Markierungen gehörenden Zahlen an. Punkt F = ?
|
33
|
|
|
|
|
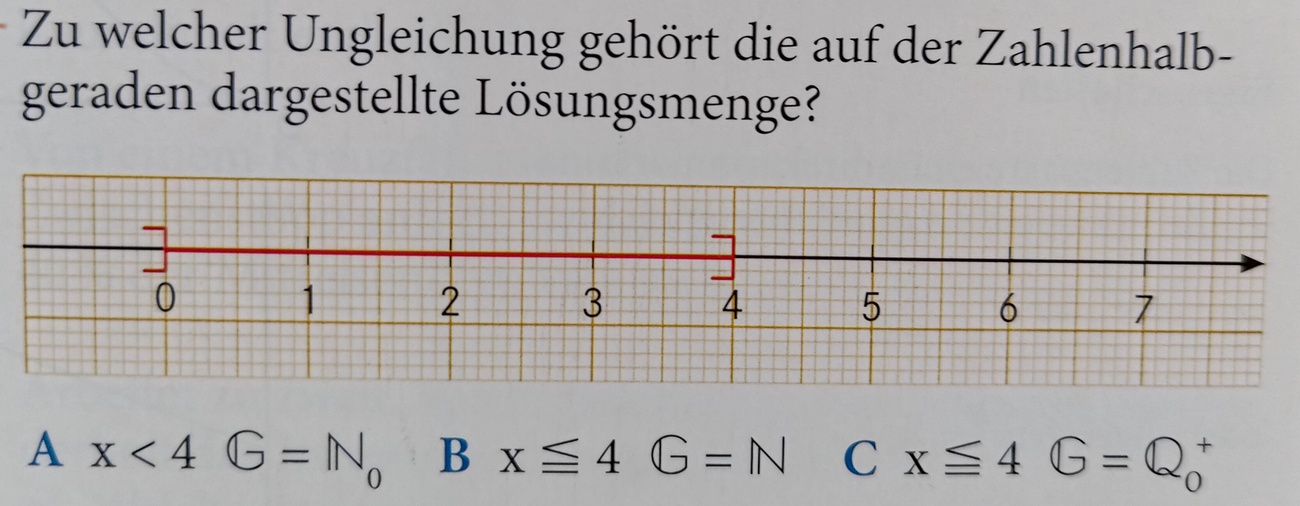
Zu welcher Ungleichung gehört die auf der Zahlenhalbgeraden dargestellte Lösungsmenge? Gib den Buchstaben der Lösung an!
|
B
|
|
|
×
|
|
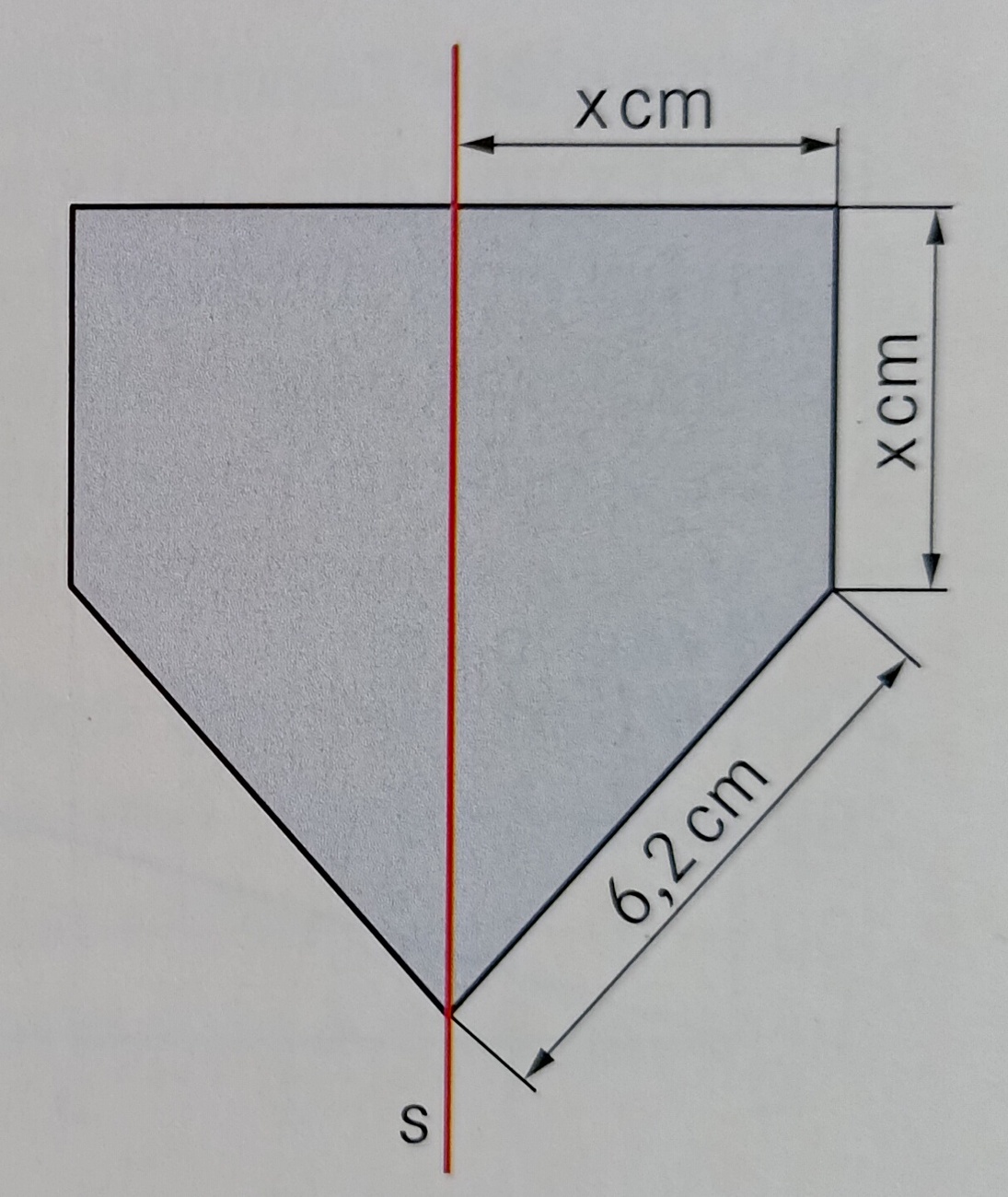
Der Umfang der achsensymmetrischen Figur beträgt 28,8 cm. Berechne den Wert von x!
|
x = 4,1 cm
|
|
|
×
|
|
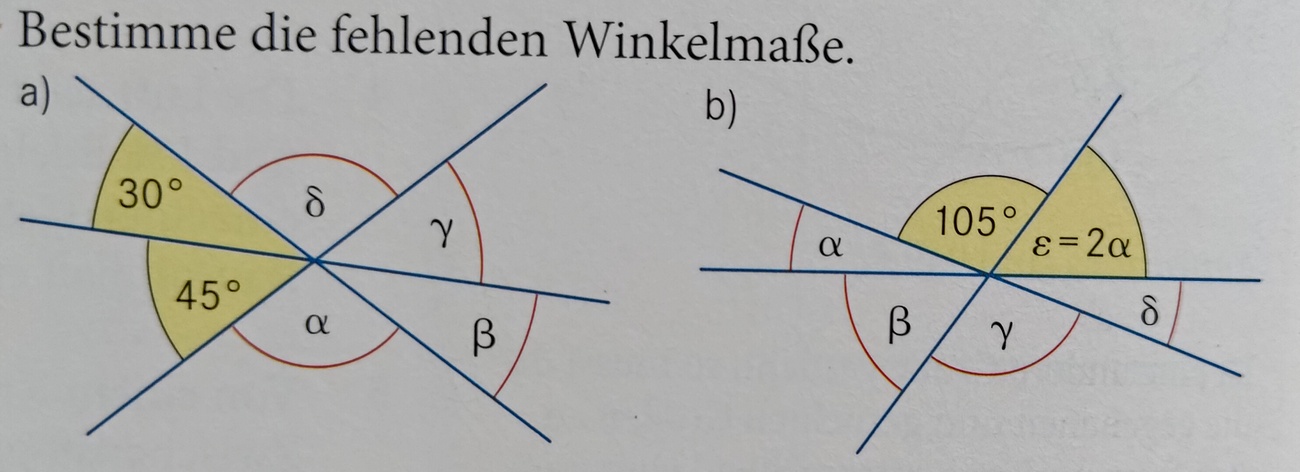
Bestimme die fehlenden Winkelmaße in Figur a)
|
α=105°, β=30°, γ=45°, δ=105°
|
|
|
×
|
Bestimme die fehlenden Winkelmaße in Figur b)
|
α=25°, β=50°, γ=45°, δ=25°, ε=50°
|
|
|
|
|
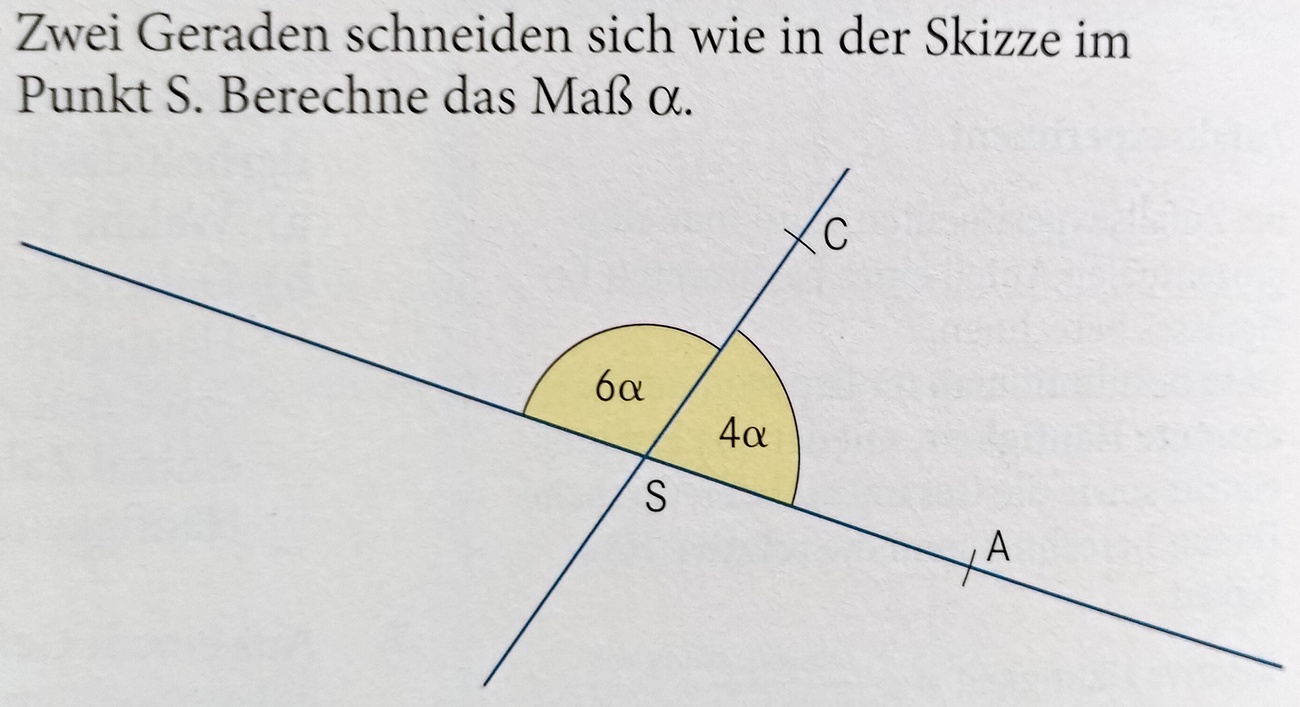
Zwei Geraden schneiden sich wie in der Abbildung im Punkt S. Berechne das Maß α!
|
α = 18°
|
|
|
×
|
|
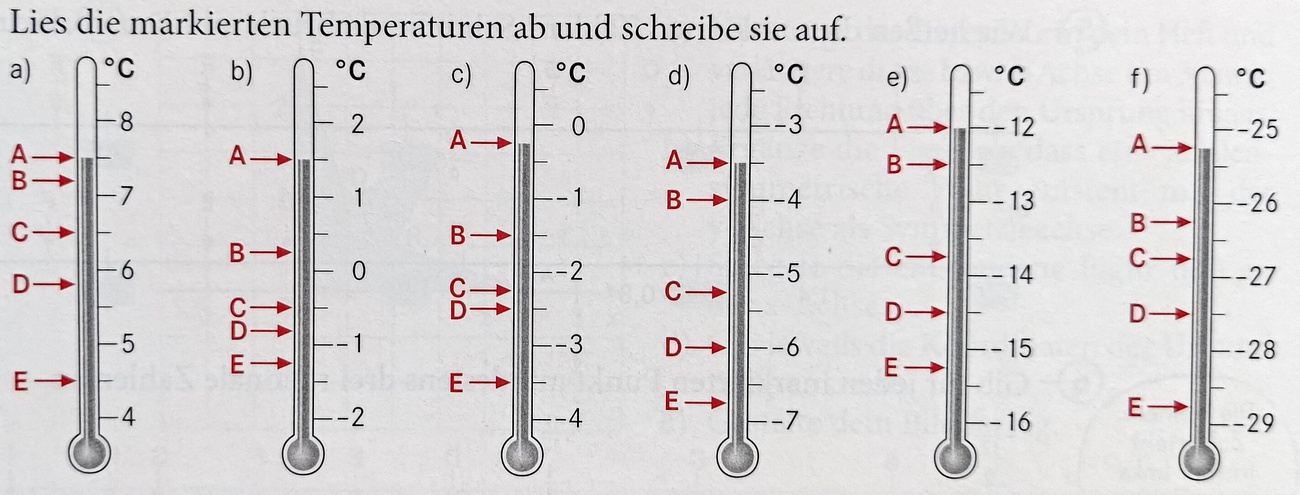
Welche Temperatur markiert der Punkt C in Teilaufgabe a?
|
6,5°C
|
|
|
×
|
Welche Temperatur markiert der Punkt A in Teilaufgabe b?
|
1,5°C
|
|
|
|
Welche Temperatur markiert der Punkt B in Teilaufgabe c?
|
-1,5°C
|
|
|
|
Welche Temperatur markiert der Punkt D in Teilaufgabe f?
|
-27,5°C
|
|
|
|
|
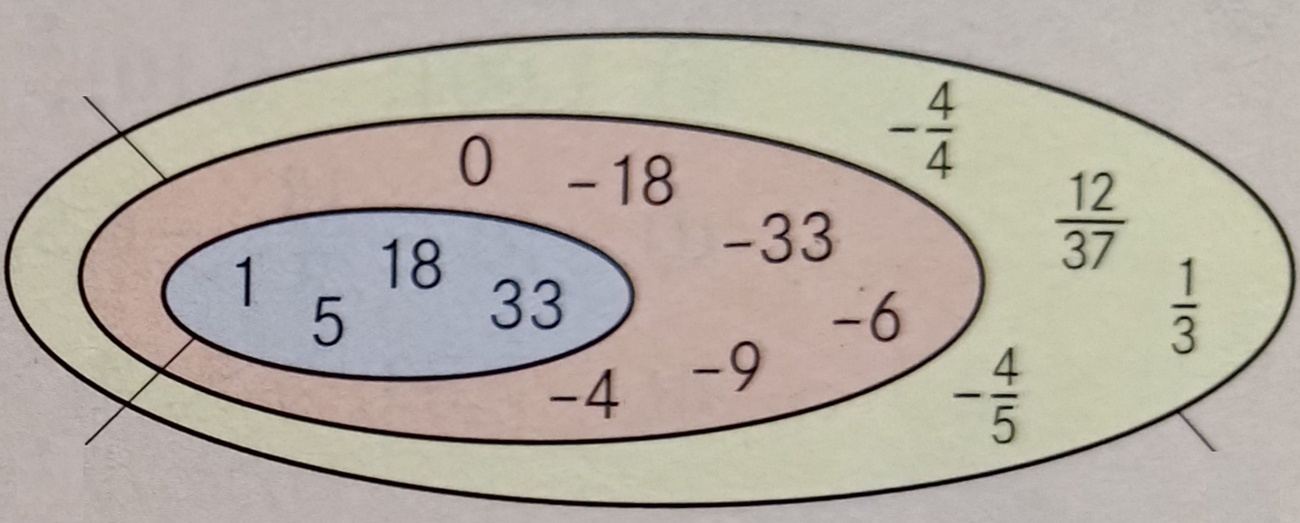
Ordne die Zahlenmenge Z der ganzen Zahlen anhand der Zahlenbeispiele in den farbigen Ellipsen einer Farbe zu!
|
orange
|
|
|
×
|
Ordne die Zahlenmenge N der natürlichen Zahlen anhand der Zahlenbeispiele in den farbigen Ellipsen einer Farbe zu!
|
blau
|
|
|
|
Ordne die Zahlenmenge Q der rationalen Zahlen anhand der Zahlenbeispiele in den farbigen Ellipsen einer Farbe zu!
|
gelb
|
|
|
|
|
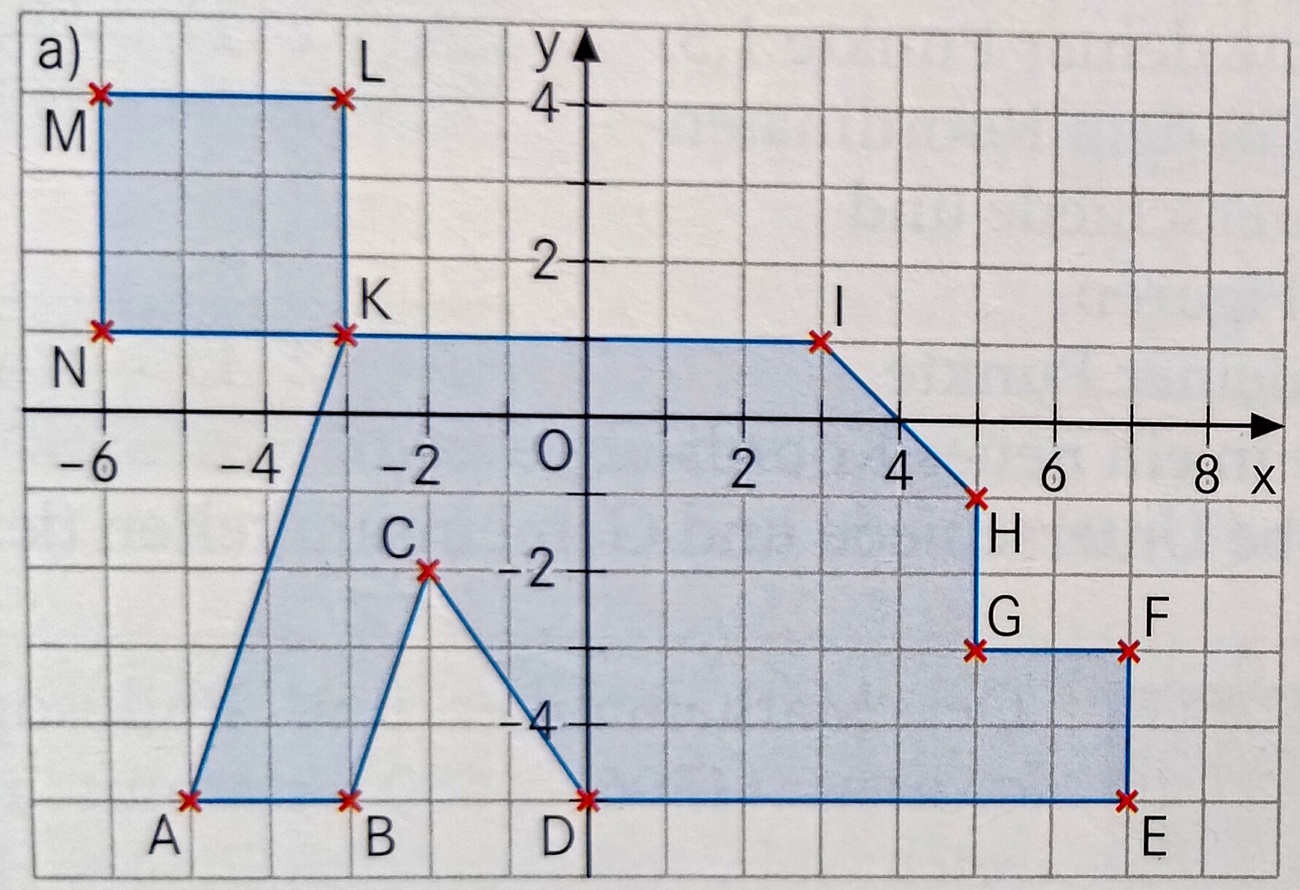
Gib die Koordinaten des Punktes K für Teilaufgabe a) an!
|
K=(-3;1)
|
|
|
×
|
Gib die Koordinaten des Punktes G für Teilaufgabe a) an!
|
G=(5;-3)
|
|
|
|
Gib die Koordinaten des Punktes A für Teilaufgabe a) an!
|
A=(-5;-5)
|
|
|
|
|
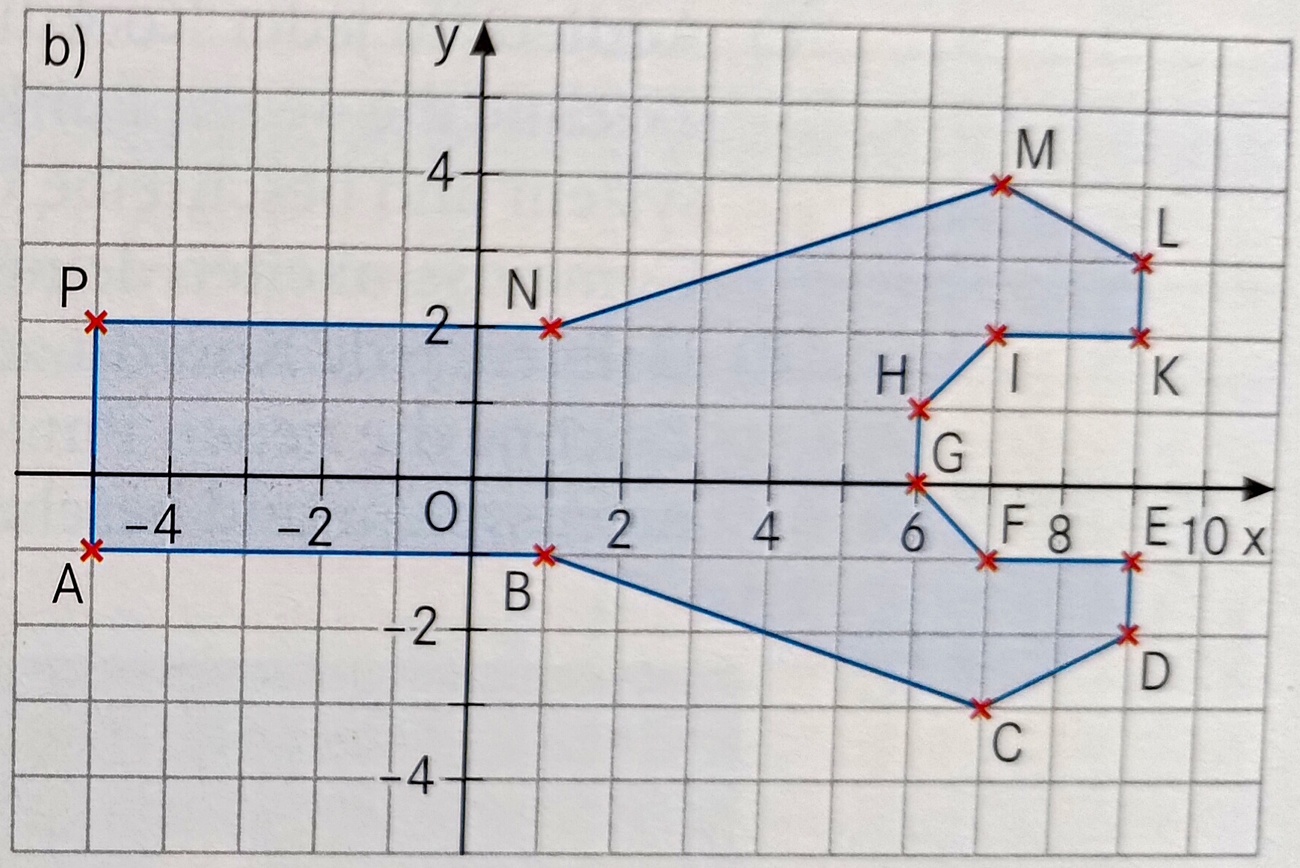
Gib die Koordinaten des Punktes M für Teilaufgabe b) an!
|
M=(7;4)
|
|
|
×
|
|
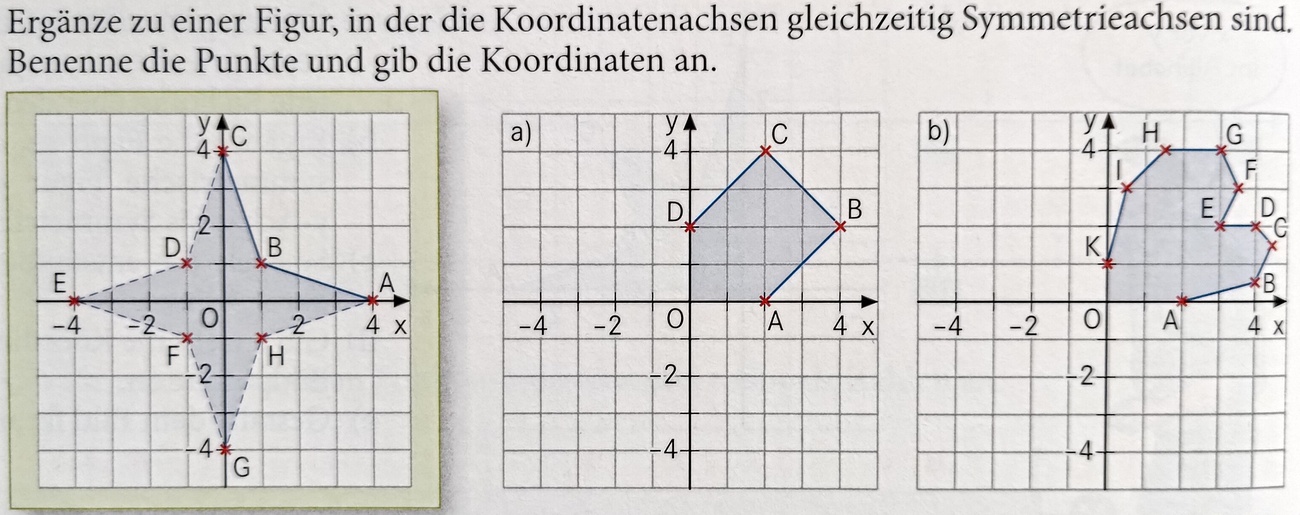
Ergänze die Figur aus Teilaufgabe a) so wie links im Bild zu sehen. Was für eine Figur entsteht?
|
Ein Kreuz, bzw. Andreaskreuz
|
|
|
×
|
Ergänze die Figur aus Teilaufgabe b) so wie links im Bild zu sehen und führe die Nummerierung der Punkte ebenso weiter wie links zu sehen. Welche Koordinaten hat der Punkt L?
|
L=(-0,5;3)
|
|
|
|
|
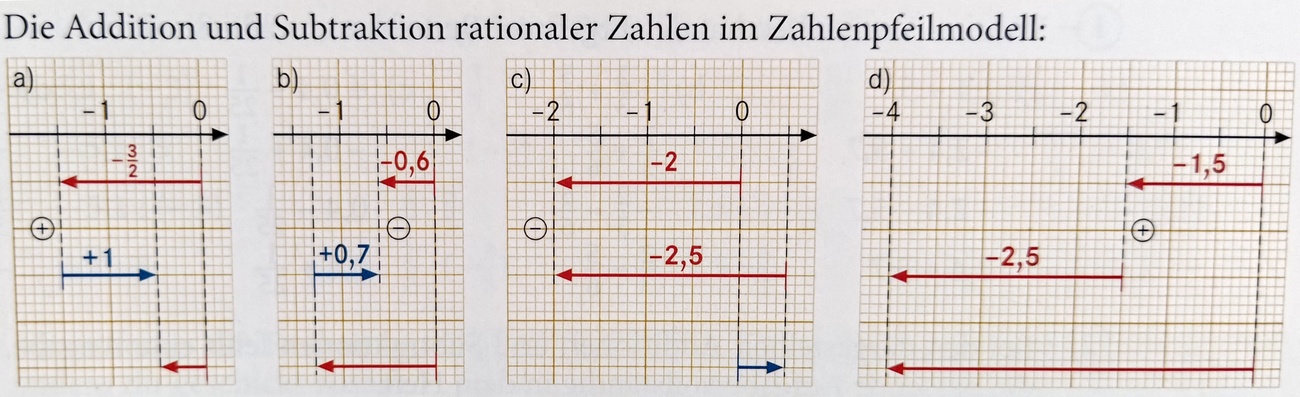
Wie lautet die in Teilaufgabe b) abgebildete Rechnung? Gib auch gleich das Ergebnis mit an!
|
-0,6-0,7=-1,3
|
|
|
×
|
Wie lautet die in Teilaufgabe c) abgebildete Rechnung? Gib auch gleich das Ergebnis mit an!
|
-2-(-2,5)=0,5
|
|
|
|
Wie lautet die in Teilaufgabe d) abgebildete Rechnung? Gib auch gleich das Ergebnis mit an!
|
-1,5+(-2,5)=-4
|
|
|
|
|
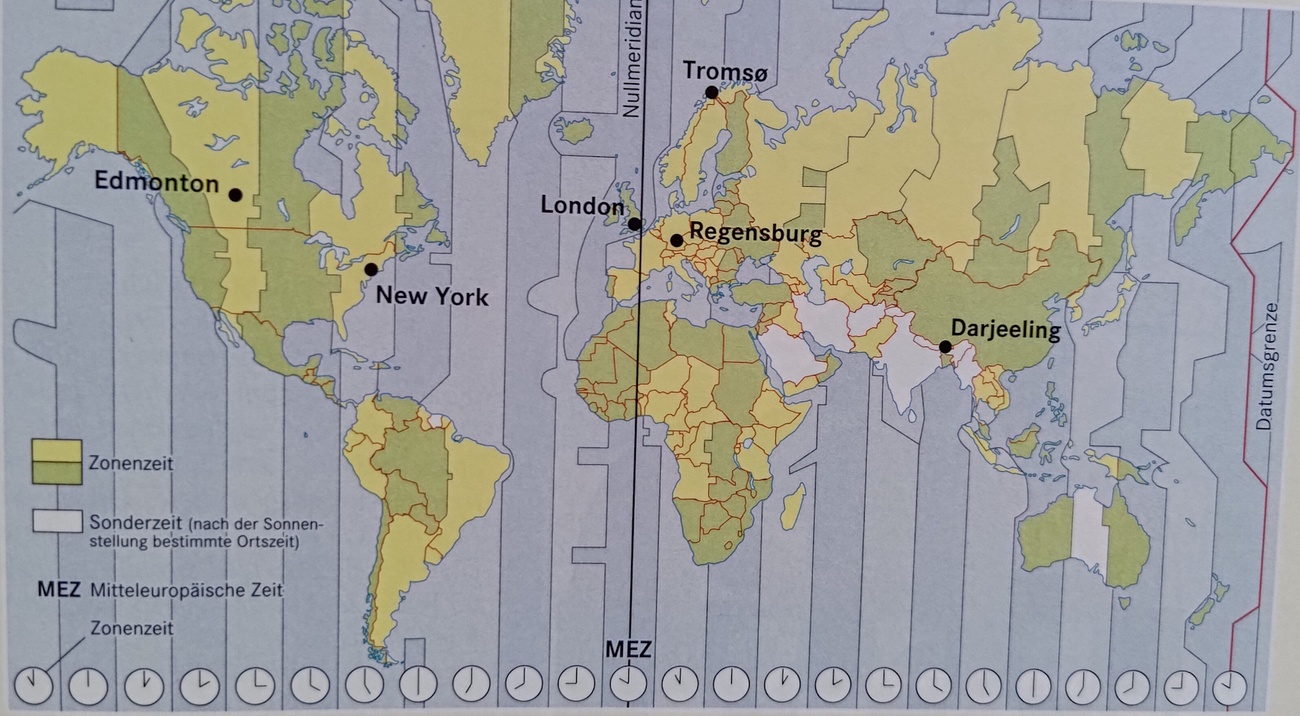
Die Schulkinder der 7b) des Goethe-Gymnasiums in Regensburg wollen eine Videokonferenz mit Schülern der Partnerschulen in den markierten Orten auf der Karte machen. Sie planen die Konferenz für 10 Uhr vormittags MEZ. Ist das ein günstiger Zeitpunkt? Begründe kurz und knapp.
|
nein, weil es in Edmonton dann 3 Uhr morgens ist.
|
Der Schüler muss erkennen, dass die Zeit unpraktisch ist, da es in Edmonton zu früh ist.
|
|
×
|
Die Schulkinder der 7b) des Goethe-Gymnasiums in Regensburg wollen eine Videokonferenz mit Schülern der Partnerschulen in den markierten Orten auf der Karte machen. Schlage eine Uhrzeit nach MEZ für die Konferenz vor, an der alle Schüler der Partnerschulen typischerweise wach sind.
|
14 Uhr MEZ. Dann ist es in Edmonton 7 Uhr morgens und in Darjeeling 20 Uhr abends.
|
|
|
|
|
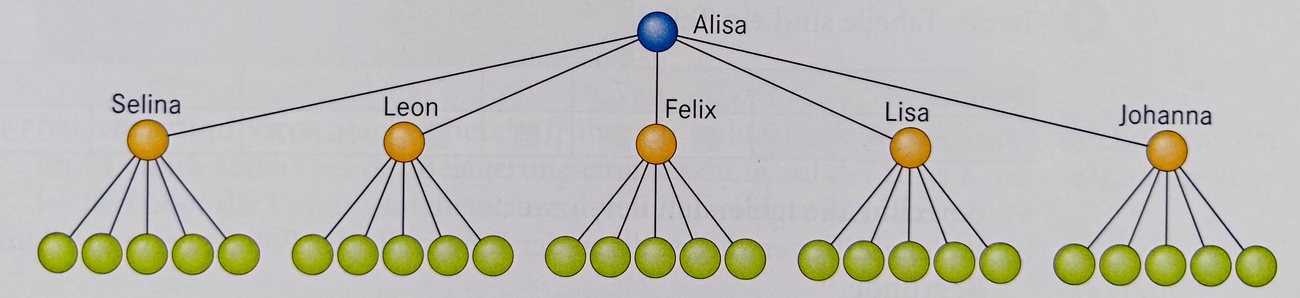
Alisa schickt eine Ketten-Email an die abgebildeten Freunde. Wie viele Empfänger bekommen die Email, nachdem Alisas Freunde die Email ebenfalls weiter verschickt haben wie abgebildet?
|
25
|
|
|
×
|
Alisa schickt eine Ketten-Email an die abgebildeten Freunde in orange (Runde 1). Diese schicken sie wiederum weiter an die grün abgebildeten Empfänger (Runde 2). Wieviele Empfänger bekommen die Email in der dritten Runde?
|
5^3 = 125
|
|
|
|
|
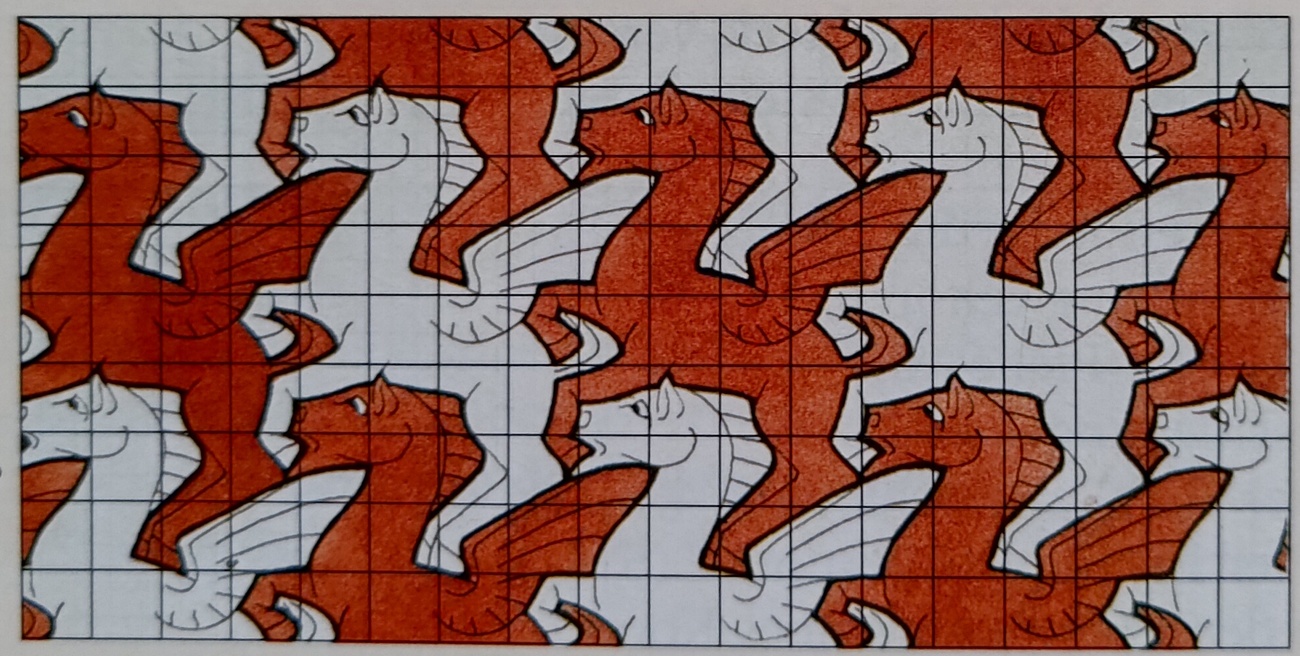
Über das Escher-Parkett ist ein Kästchenraster gelegt. Beschreibe mathematisch, wie ein weißes Pferd auf ein benachbartes rotes Pferd abgebildet werden kann!
|
Verschiebung um (4;0)
|
|
|
×
|
|
Bearbeite die im Bild abgedruckte Teilaufgabe a)
|
ja
|
|
|
×
|
Bearbeite die im Bild abgedruckte Teilaufgabe b)
|
nein, weil die Verschiebung (3;2) statt (3;1) ist
|
|
|
|
|
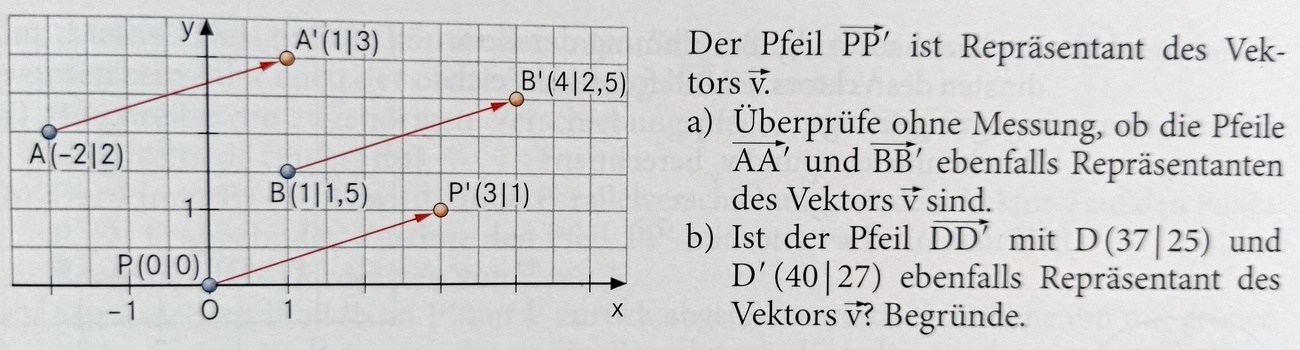
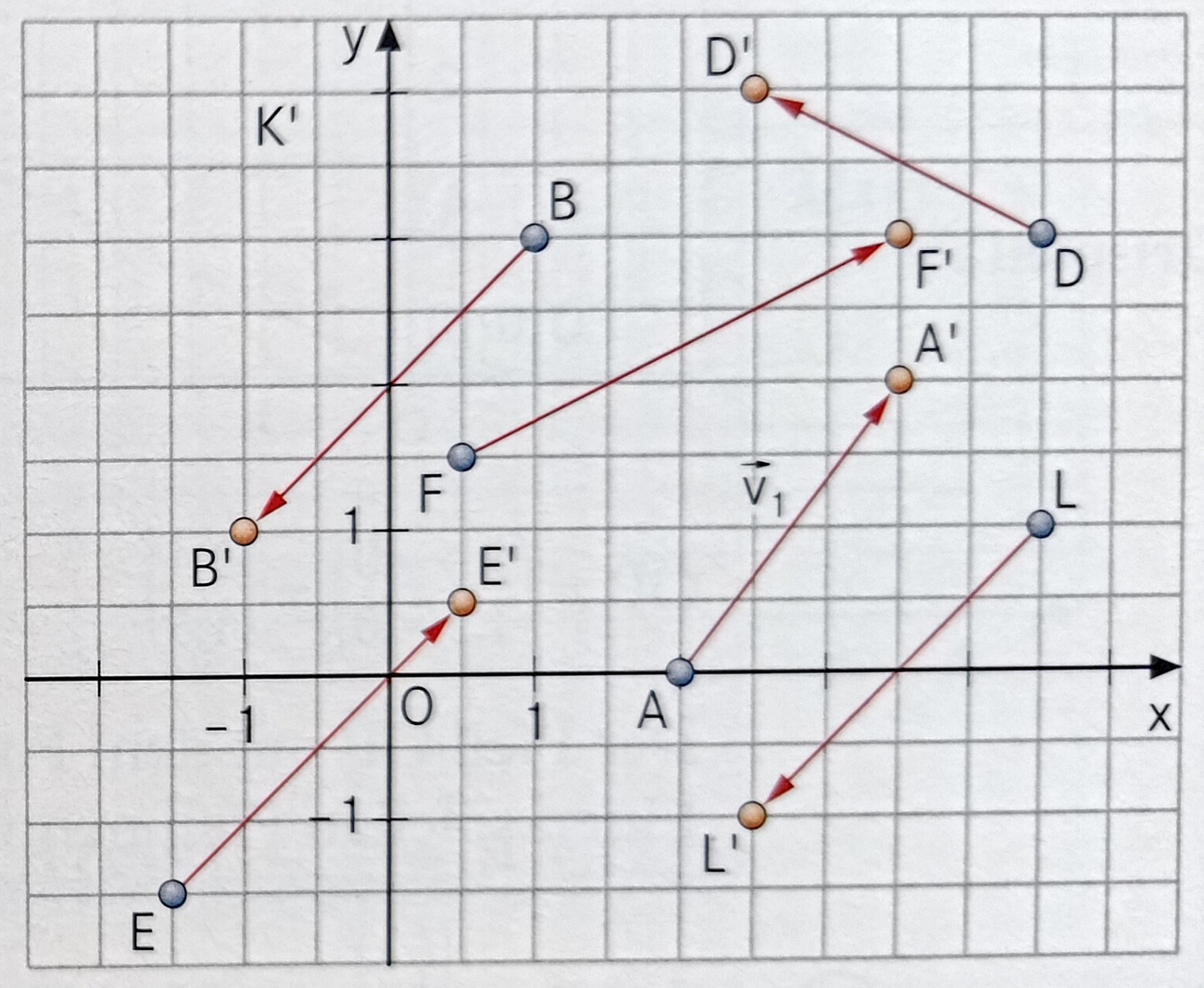
Die roten Pfeile stehen für Vektoren, die eine Verschiebung bezeichnen. Gib die Koordinaten des Vektors v1 von A nach A' an!
|
v1 = (1,5;2)
|
|
|
×
|
Die roten Pfeile stehen für Vektoren, die eine Verschiebung bezeichnen. Ein Vektor kommt zweimal vor. Nenne die Ausgangspunkte der beiden Pfeile und gib die Koordinaten des Vektors an.
|
B, L, (-2;-2)
|
|
|
|
|
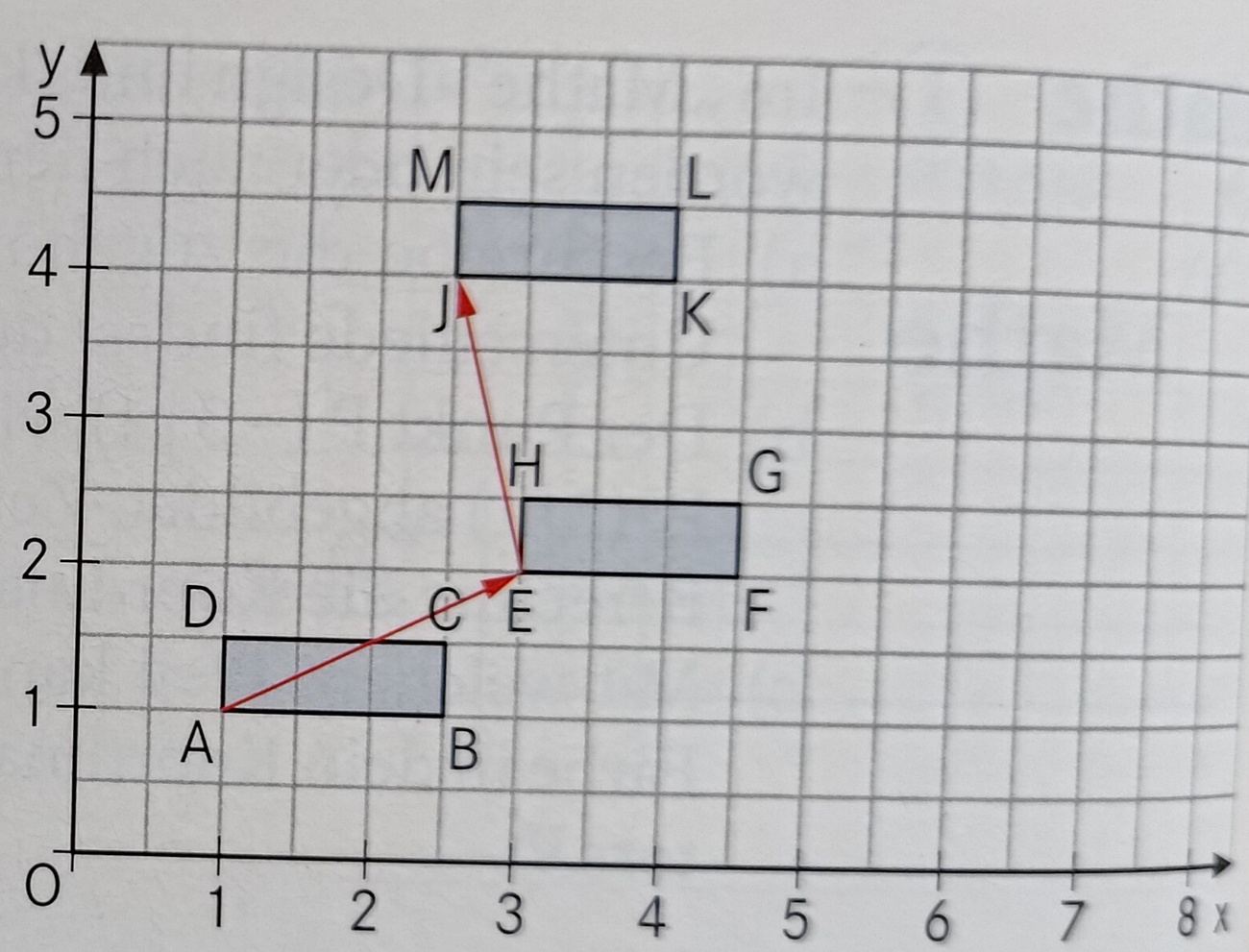
Die Rechtecke ABCD, EFGH und JKLM können durch Parallelverschiebung aufeinander abgebildet werden. Gib die Koordinaten des Vektors von A nach E (v1) an.
|
v1=(2;1)
|
|
|
×
|
Die Rechtecke ABCD, EFGH und JKLM können durch Parallelverschiebung aufeinander abgebildet werden. Gib die Koordinaten des Vektors von E nach J (v2) an.
|
v2=(-0,5;2)
|
|
|
|
Die Rechtecke ABCD, EFGH und JKLM können durch Parallelverschiebung aufeinander abgebildet werden. Gib die Koordinaten des Vektors v3 an, der direkt das Rechteck ABCD auf JKLM abbildet!
|
v3=(1,5;3)
|
|
|
|
|
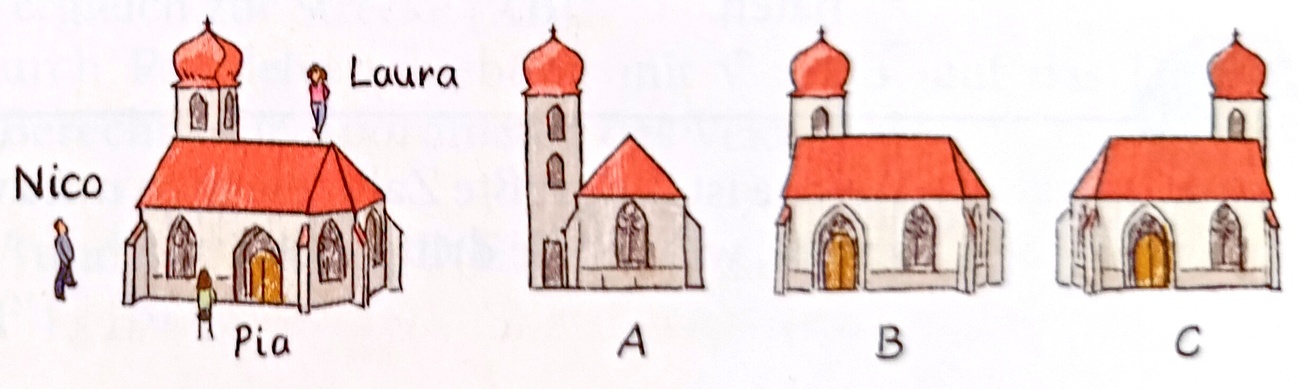
Welches der Kinder könnte die Kirche aufgrund der abgebildeten Position im linken Bild so sehen, wie dies unter A, B oder C dargestellt ist? Nenne die Namen und jeweils den Buchstaben.
|
Nico (A), Pia (B), Laura (C)
|
|
|
×
|
|
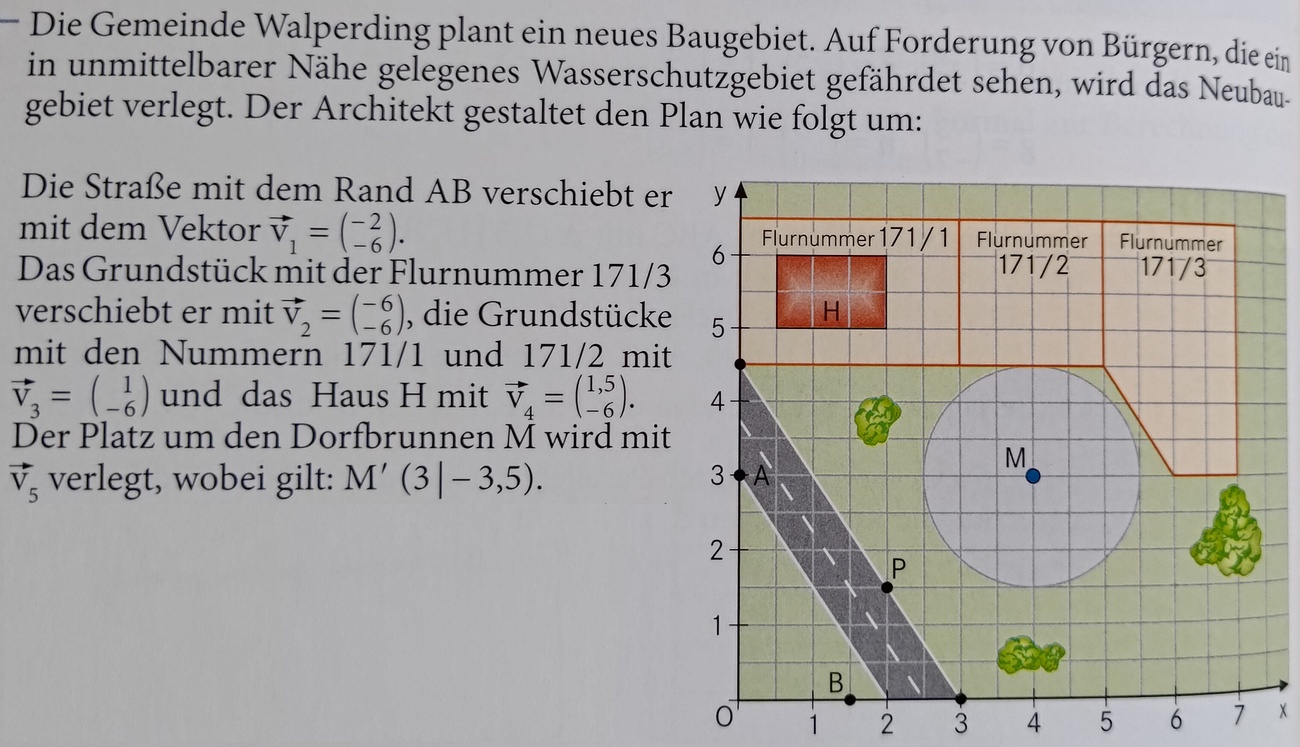
Berechne die Koordinaten von P' gemäß den Anweisungen im Bild!
|
P'=(0;-4,5)
|
|
|
×
|
Berechne die Koordinaten des Vektors v5 gemäß den Anweisungen im Bild!
|
v5 = (-1;-6,5)
|
|
|
|
|
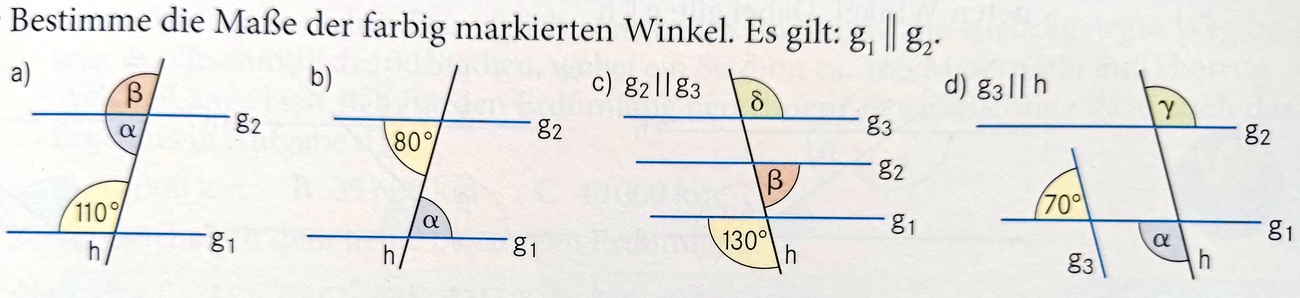
Bestimme die Maße der Winkel α und β für Teilaufgabe a)
|
α=70°, β=110°
|
|
|
×
|
Bestimme die Maße der Winkel β und δ für Teilaufgabe c)
|
β=50° und δ=130°
|
|
|
|
Bestimme die Maße der Winkel α und γ für Teilaufgabe d)
|
α=110° und γ=110°
|
|
|
|
|
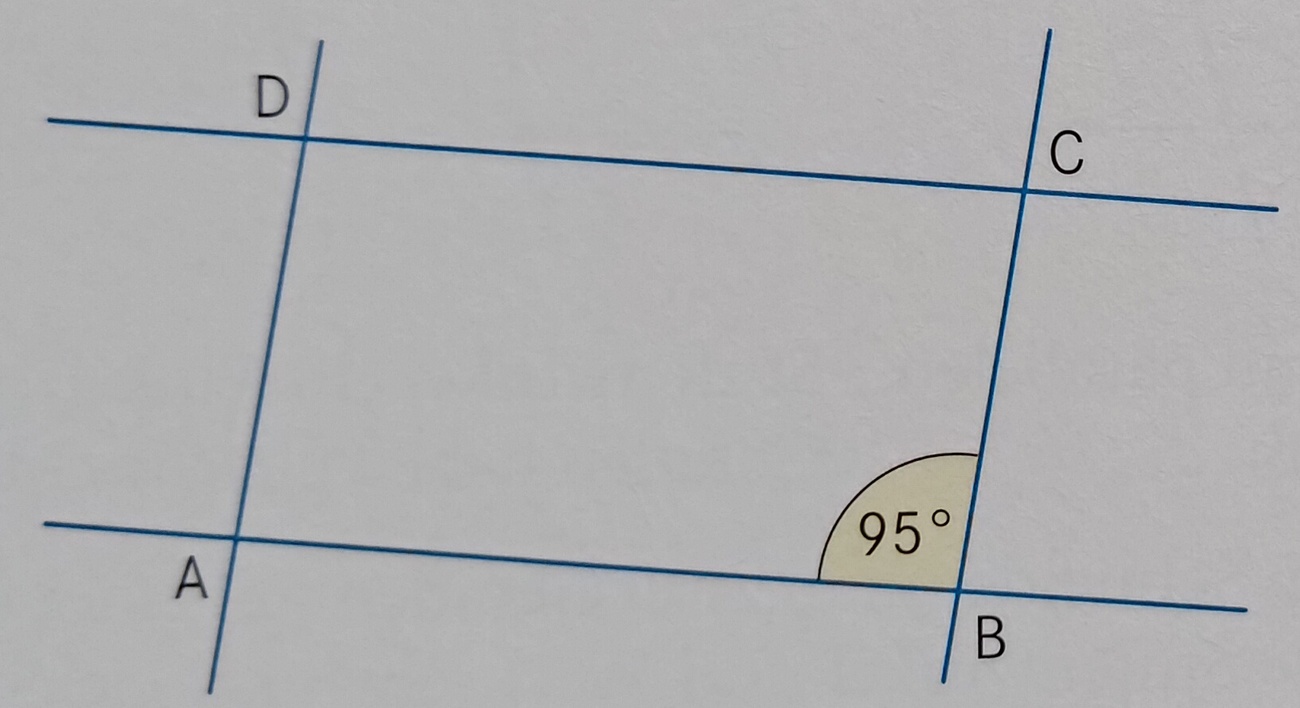
Das Viereck ABCD ist ein Parallelogramm. Bestimme die Maße der Innenwinkel.
|
α=85°, β=95°, die Winkel bei C und D sind analog
|
|
|
×
|
|
Löse Teilaufgabe a). Berechne zunächst das Maß von α und anschließend die Maße der anderen gekennzeichneten Winkel. Dabei gilt: g || h
|
α=36°, β=36°, γ=144°, δ=36°, ε=144°
|
|
|
×
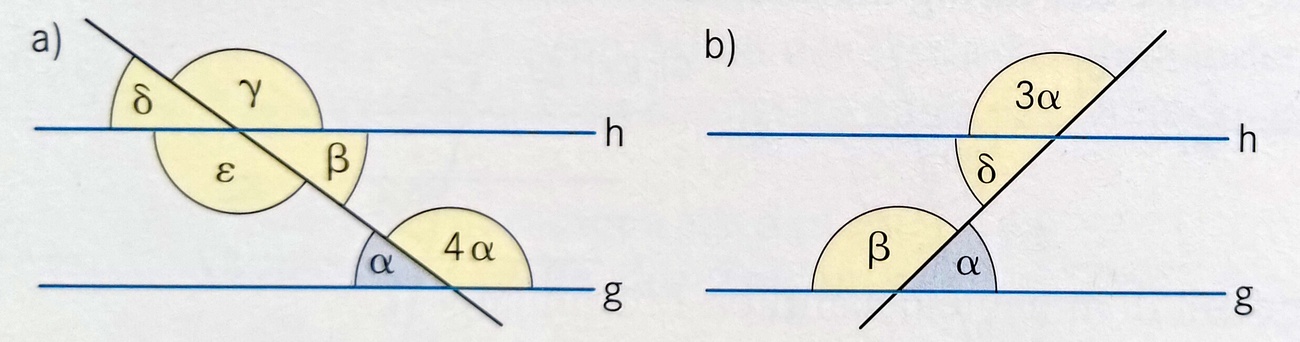
|
Löse Teilaufgabe b). Berechne zunächst das Maß von α und anschließend die Maße der anderen gekennzeichneten Winkel. Dabei gilt: g || h
|
α=45°, β=135°, δ=45°
|
|
|
|
|
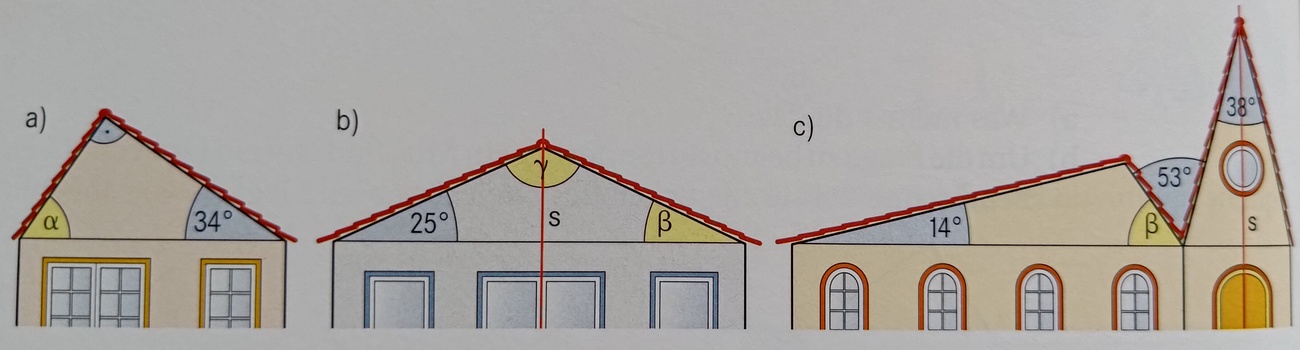
Welche Dreiecksform haben die Giebel in Teilaufgabe a) und b)?
|
a) rechtwinkliges Dreieck, b) gleichschenkliges Dreieck
|
|
|
×
|
Berechne das Maß für den Winkel α in Teilaufgabe a)
|
α=56°
|
|
|
|
Berechne das Maß für den Winkel γ in Teilaufgabe b)
|
γ=130°
|
|
|
|
Berechne das Maß für den Winkel β in Teilaufgabe c)
|
β=56°
|
|
extra schwer
|
|
|
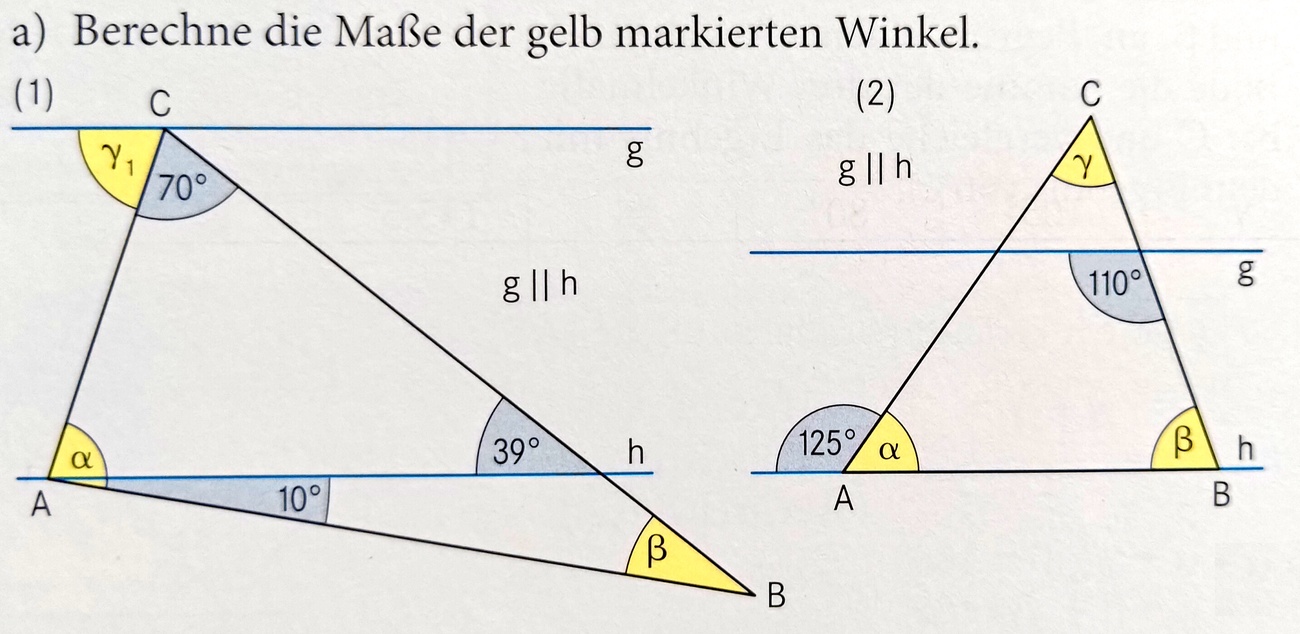
Berechne die Maße der gelb markierten Winkel in Teilaufgabe a)
|
γ1=71°, β=29°, α=81°
|
|
extra schwer
|
×
|
Berechne die Maße der gelb markierten Winkel in Teilaufgabe b)
|
α=65°, β=70°, γ=45°
|
|
|
|
|
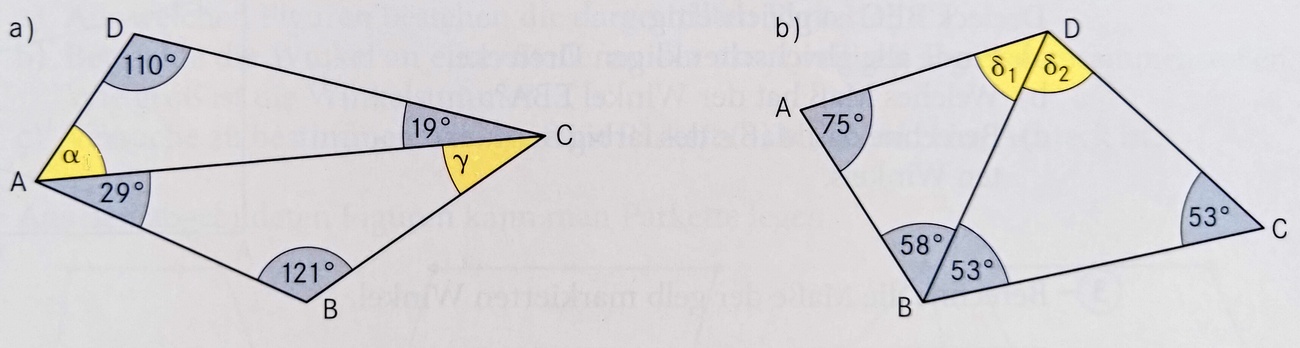
Berechne die Maße der fehlenden Winkel für Teilaufgabe a)
|
α=51°, γ=30°
|
|
|
×
|
Berechne die Maße der fehlenden Winkel für Teilaufgabe b)
|
δ1=47°, δ2=74°,
|
|
|
|
|
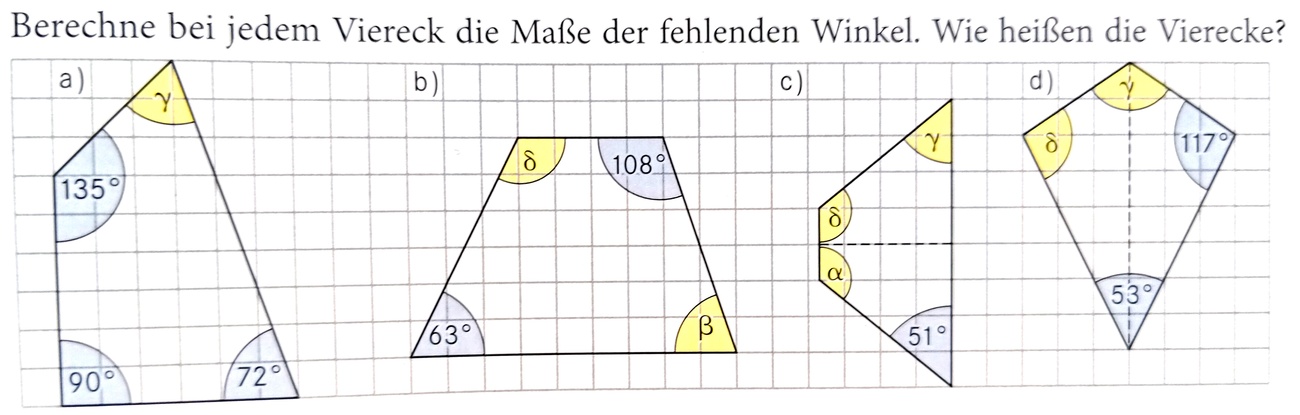
Berechne für Teilaufgabe a) das Maß für den Winkel γ!
|
γ=63°
|
|
ab hier Vierecke und nicht mehr Dreiecke
|
×
|
Berechne für Teilaufgabe b) die Maße für die Winkel β und δ!
|
β=117°, δ=72°
|
|
|
|
Berechne für Teilaufgabe c) die Maße für die Winkel δ und γ!
|
δ=129°, γ=51°
|
|
|
|
Berechne für Teilaufgabe d) die Maße für die Winkel δ und γ!
|
δ=117°, γ=73°
|
|
|
|
|
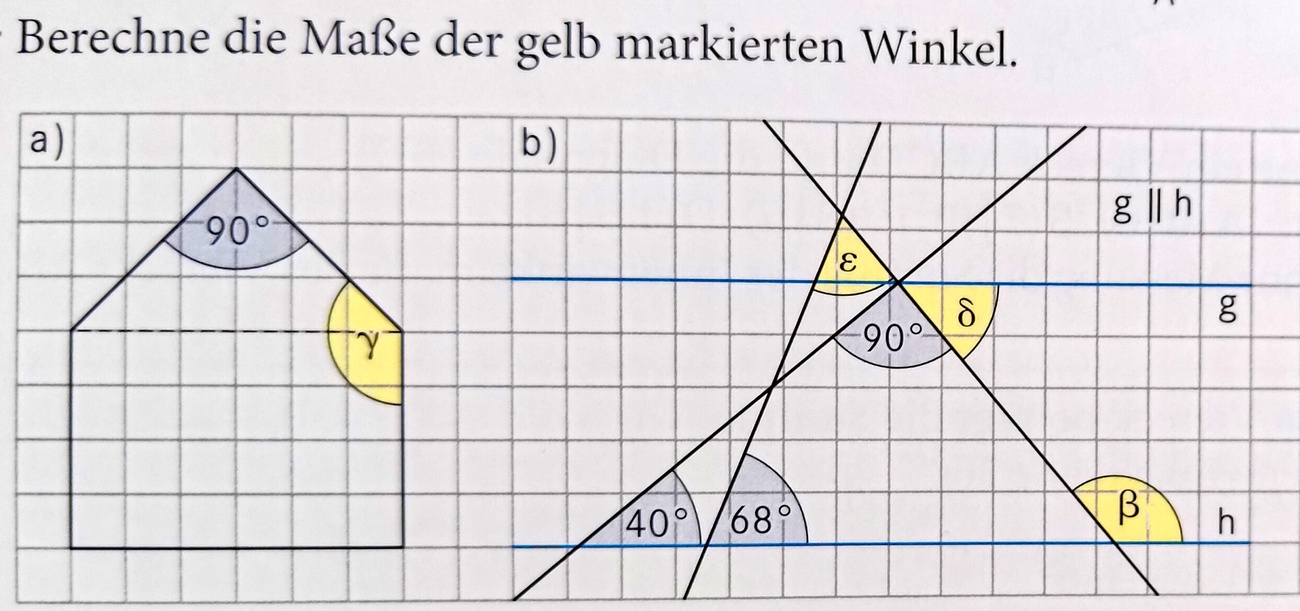
Berechne für Teilaufgabe a) das Maß für den Winkel γ!
|
γ=135°
|
|
|
×
|
Berechne für Teilaufgabe b) die Maße für die Winkel β, δ und ε!
|
β=130°, δ=50° und ε=62°
|
|
|
|
|
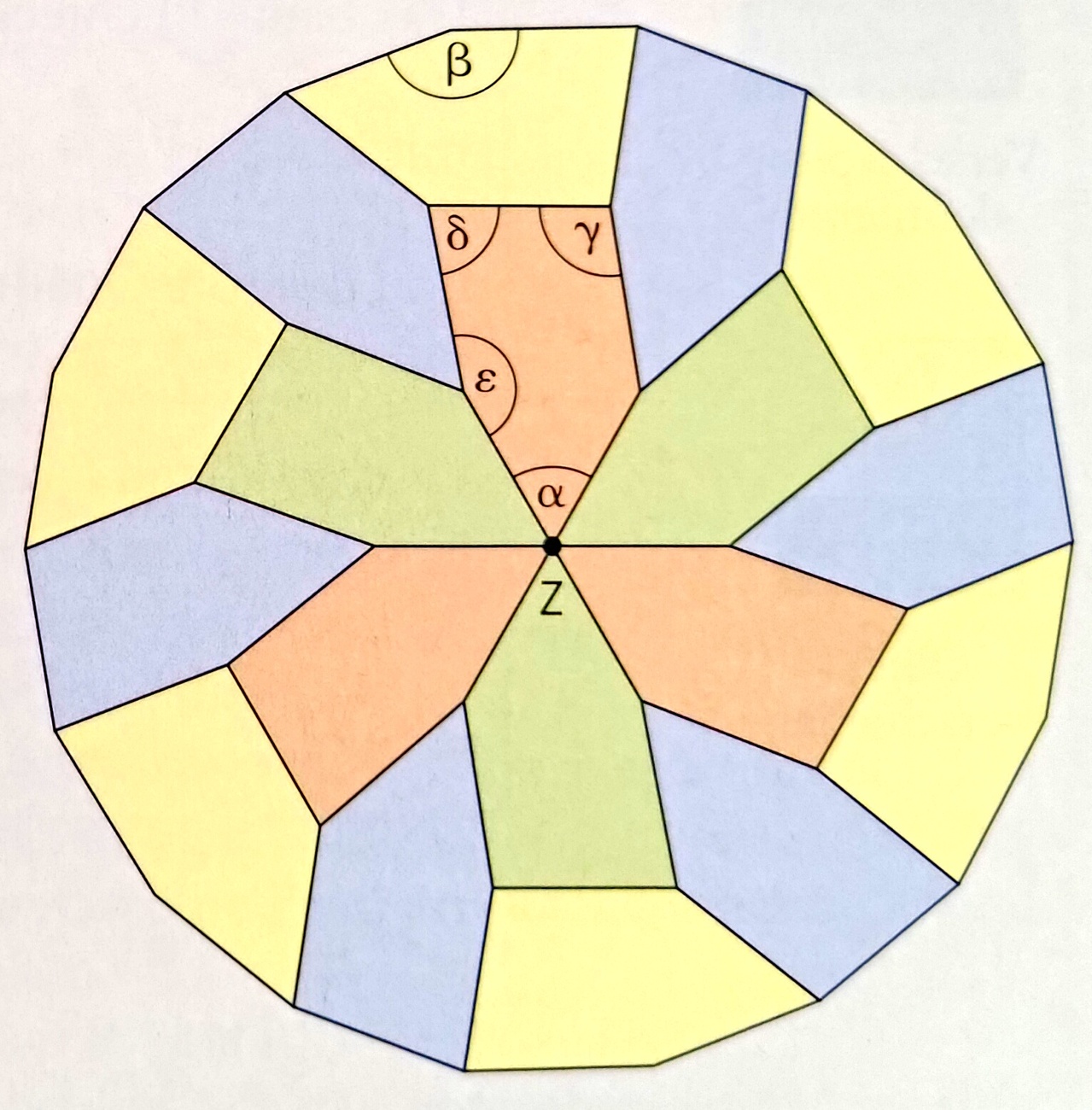
Berechne das Winkelmaß für α
|
α=60°
|
|
|
×
|
Berechne das Winkelmaß für β
|
β=160°
|
|
|
|
ε=β und δ=β/2. Berechne das Winkelmaß für γ!
|
γ=100°
|
|
extra schwer
|
|
|
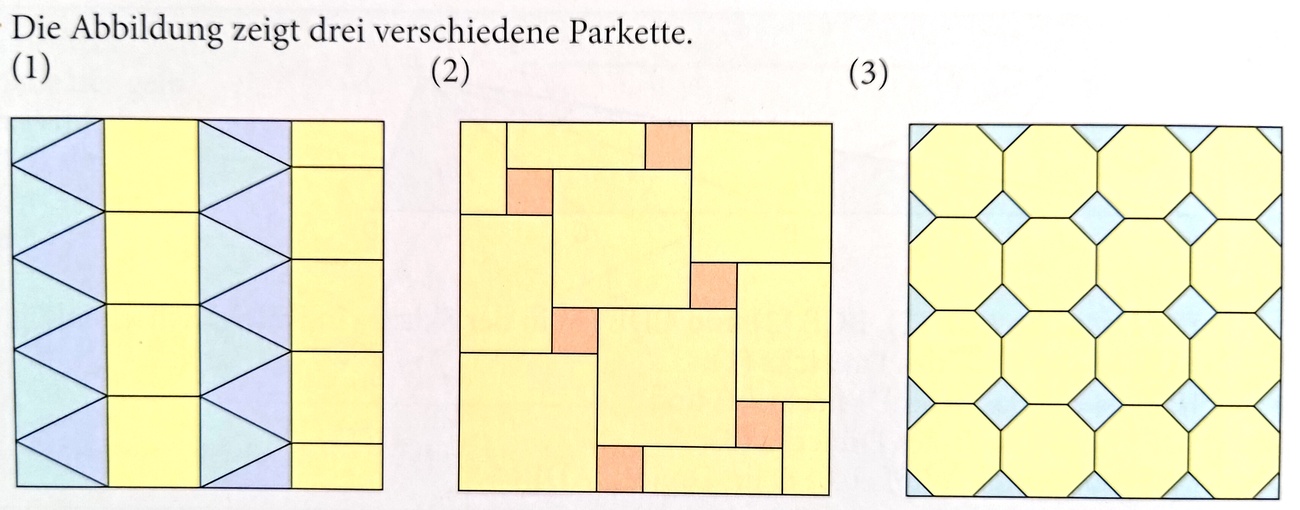
Aus welchen Figuren besteht das Parkett in Abbildung (1)?
|
Dreiecke und Quadrate
|
|
|
×
|
Aus welchen Figuren besteht das Parkett in Abbildung (2)?
|
Quadrate
|
|
Die als Rechteck erscheinenden Teile sind abgeschnittene Quadrate
|
|
Aus welchen Figuren besteht das Parkett in Abbildung (3)?
|
s
|
|
|
|
|
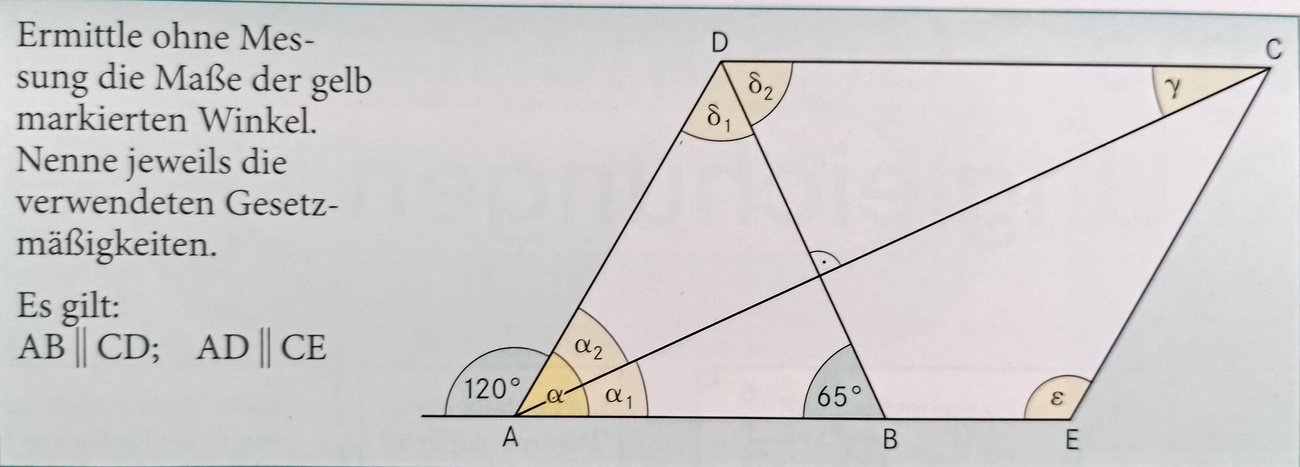
Ermittle die Maße für die Winkel α, δ1 und α2!
|
α=60°, δ1=55°, α2=35°
|
|
|
×
|
α=60°, δ1=55°, α2=35°. Ermittle die Maße für die Winkel δ2, α1 und ε!
|
δ2=65°, α1=γ=25°, ε=120°
|
|
|
|
|
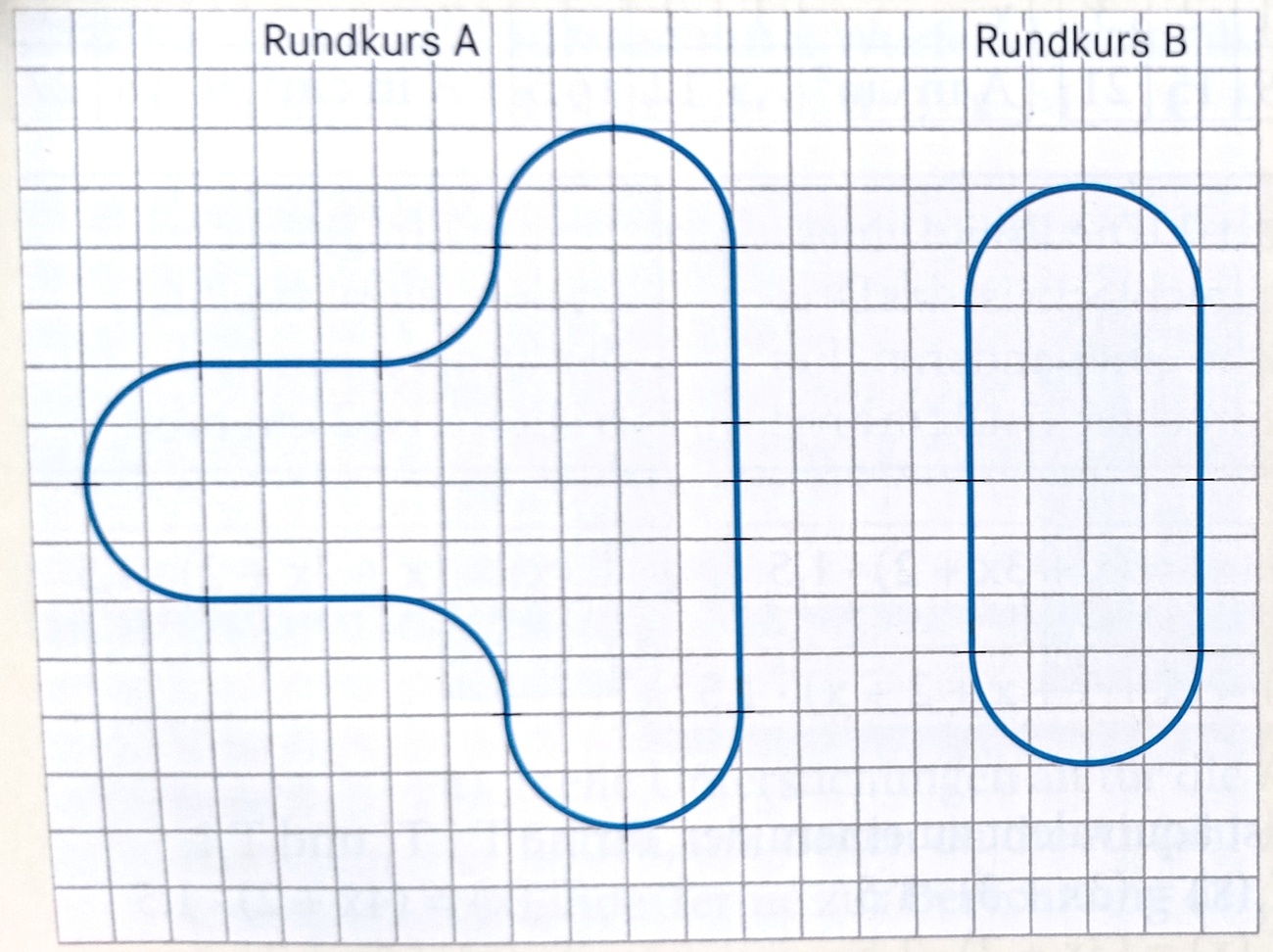
Gib die Länge des Rundkurses A an. Ein Kästchen entspricht einer Einheit. Rechne mit Π als Variable, nicht als Zahl.
|
6Π+14
|
|
|
×
|
Gib die Länge des Rundkurses B an. Ein Kästchen entspricht einer Einheit. Rechne mit Π als Variable, nicht als Zahl.
|
4Π+12
|
|
|
|
|
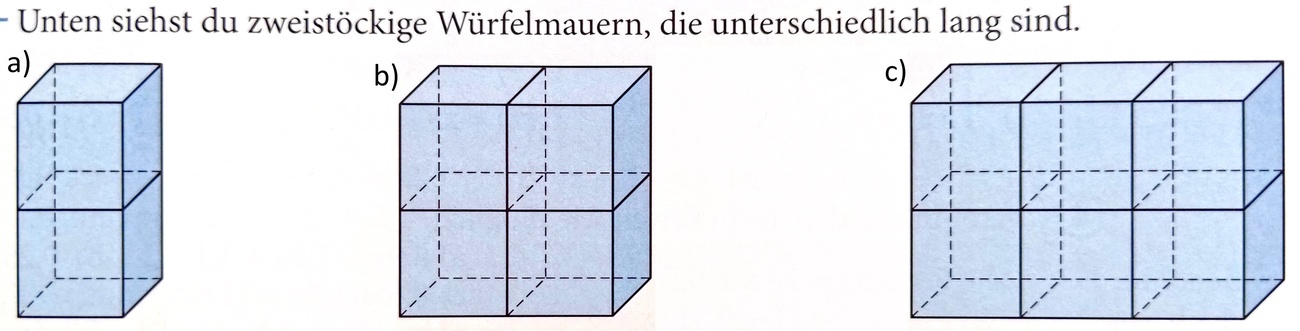
Wie viele aus der Perspektive des Betrachters sichtbare Flächen gibt es für Teilaufgabe a)?
|
5
|
|
|
×
|
Wie viele aus der Perspektive des Betrachters verdeckte Flächen gibt es für Teilaufgabe a)?
|
6
|
|
|
|
Wie viele aus der Perspektive des Betrachters sichtbare Flächen gibt es für Teilaufgabe b)?
|
8
|
|
|
|
Wie viele aus der Perspektive des Betrachters verdeckte Flächen gibt es für Teilaufgabe b)?
|
10
|
|
|
|
Wie viele aus der Perspektive des Betrachters sichtbare Flächen gibt es für Teilaufgabe c)?
|
11
|
|
|
|
Wie viele aus der Perspektive des Betrachters verdeckte Flächen gibt es für Teilaufgabe c)?
|
14
|
|
|
|
Erstelle eine Term mit der Variable n für die Anzahl nebeneinander liegender Würfel, mit dem du die Anzahl der aus der Perspektive des Betrachters sichtbaren Flächen für beliebe zweistöckige Würfelmauern berechnen kannst.
|
3n+2
|
|
evtl. auswendig gelerntes Wissen
|
|
Erstelle eine Term mit der Variable n für die Anzahl nebeneinander liegender Würfel, mit dem du die Anzahl der aus der Perspektive des Betrachters verdeckten Flächen für beliebe zweistöckige Würfelmauern berechnen kannst.
|
4n+2
|
|
evtl. auswendig gelerntes Wissen
|
|
|
Ergänze die Tabelle aus Teilaufgabe a) für 3, 4 und 5 Würfel
|
Anzahl sichtbarer Quadrate = 13, 17, 21
|
|
|
×

|
Für Türme mit der Höhe 1, 2, 3, 4, 5 ergeben sich die sichtbaren Quadrate 5, 9, 13, 17, 21. Erstelle einen Term mit der Variablen x für die Anzahl der übereinander gestapelten Würfel, mit der du die Anzahl der sichtbaren Quadrate für beliebige x berechnen kannst!
|
(x-1)*4+5
|
|
|
|
Erstelle einen Term mit der Variablen x für die Anzahl der übereinander gestapelten Würfel, mit der du die Anzahl der sichtbaren Flächen für beliebige x berechnen kannst!
|
(x-1)*4+5
|
|
|
|
|
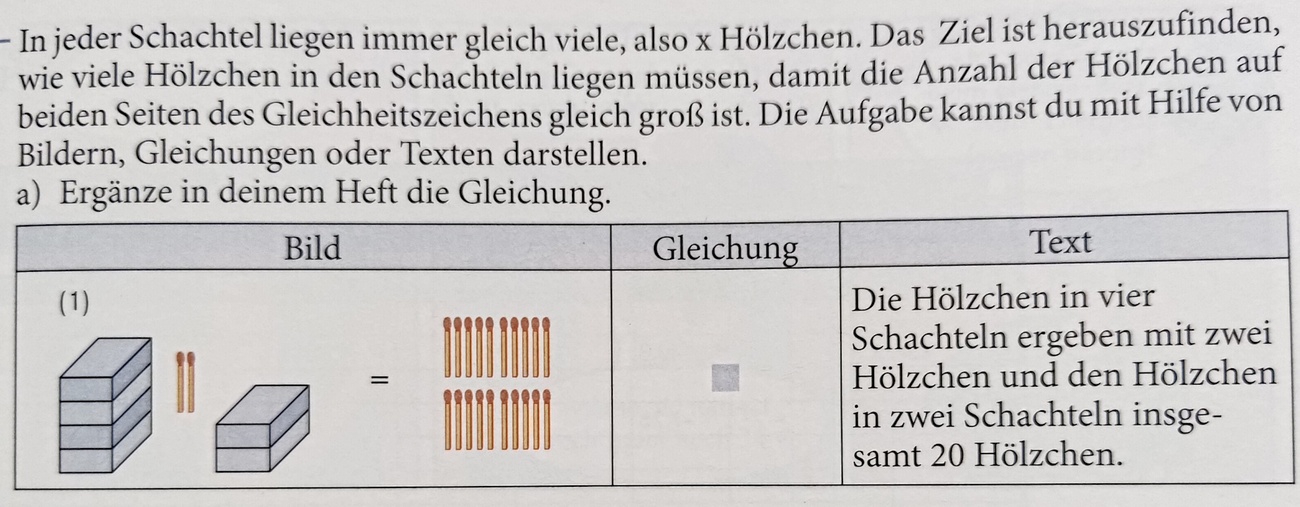
Erstelle die Gleichung mit x als Variable für die Anzahl der Hölzchen pro Schachtel
|
6x+2=20
|
|
|
×
|
Wie viele Hölzchen sind in einer Schachtel, damit die Gleichung stimmt?
|
x=3
|
|
|
|
|
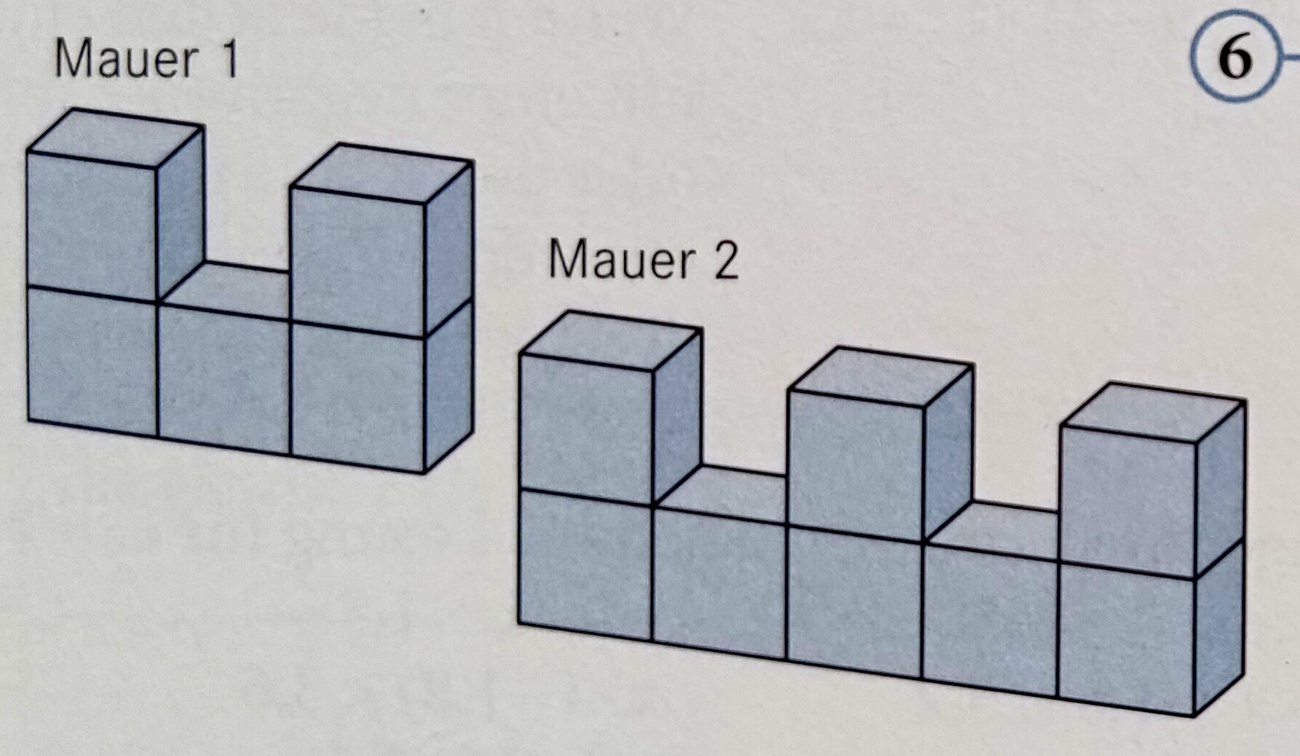
Die Abbildung zeigt eine Folge von Würfelmauern. Aus wie vielen Würfeln besteht die Mauer 1?
|
5
|
|
|
×
|
Die Abbildung zeigt eine Folge von Würfelmauern. Aus wie vielen Würfeln besteht die Mauer 2?
|
8
|
|
|
|
Die Abbildung zeigt eine Folge von Würfelmauern. Aus wie vielen Würfeln würde die nicht abgebildete Mauer 3 als logische Fortsetzung der Reihe bestehen?
|
11
|
|
|
|
Die Abbildung zeigt eine Folge von Würfelmauern. Erstelle einen Term mit der Variablen x, mit dem du für eine beliebige Mauer x die Anzahl der benötigten Würfel berechnen kannst!
|
3x+2
|
|
|
|
|
Familie Flott wohnt in einem Altbau. Hier ist ihr Stromkreis für die Steckdosen in der Küche mit 10A bei 230V abgesichert. Welche Geräte können außer der Kaffeemaschine noch genutzt werden, um die zulässige Höchstleistung für die Sicherung nicht zu überschreiten? Nenne drei Kombinationen von Geräten, die jeweils das Maximum an zulässigem Strom verbrauchen.
|
1) Kaffeemaschine + Mikrowelle + Entsafter
2) Kaffeemaschine + Wasserkocher + Mixer + Entsafter
3) Kaffeemaschine + Toaster + Mixer + Entsafter
|
|
|
×

|
|
Löse Teilaufgabe a) aus dem Bild. Antworte nur mit einem Buchstaben.
|
B
|
|
|
×
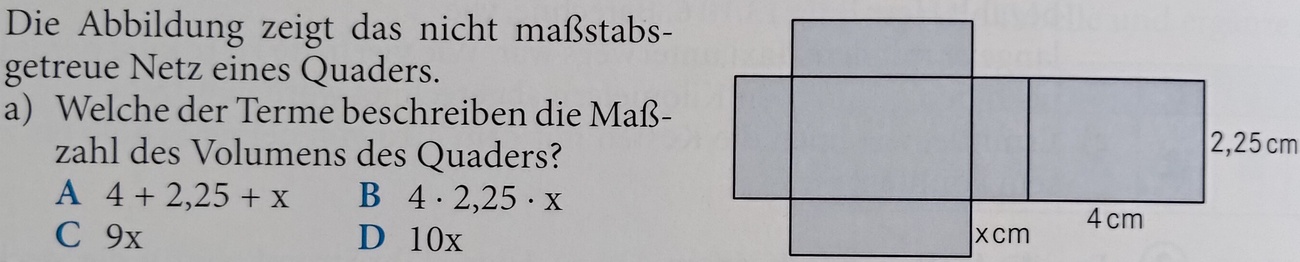
|
Das Volumen des Quaders beträgt 27 cm3. Berechne den Wert von x.
|
x=3
|
|
|
|
|
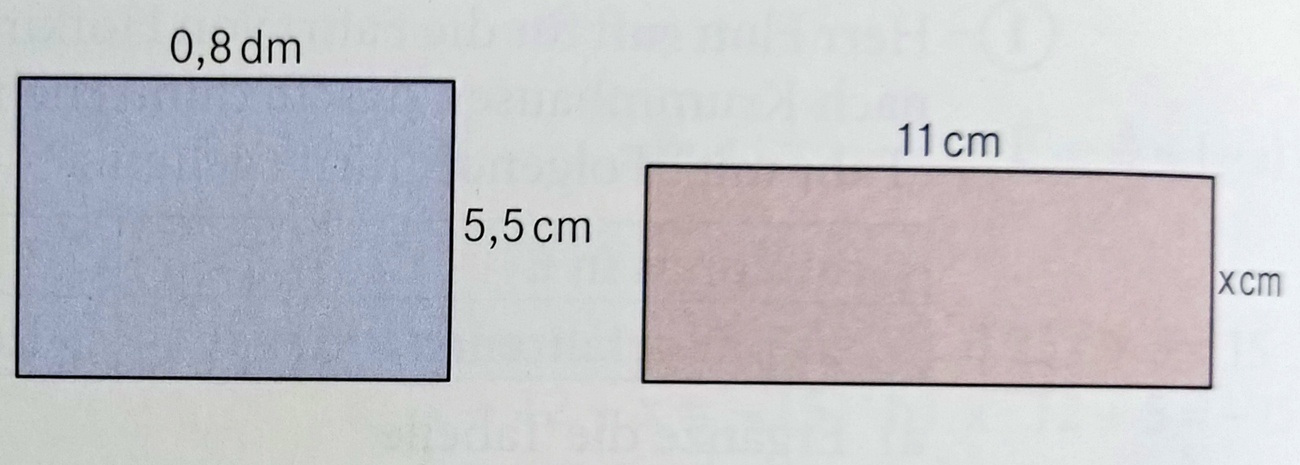
Das abgebildete blaue Rechteck soll in das flächengleiche rote Rechteck umgewandelt werden. Berechne den Wert von x.
|
x=4
|
|
|
×
|
Das abgebildete blaue Rechteck soll in das flächengleiche rote Rechteck umgewandelt werden. Wie verhält sich der Umfang des roten Rechtecks im Vergleich zum blauen?
|
er erhöht sich (von 27cm auf 30cm)
|
|
|
|
|
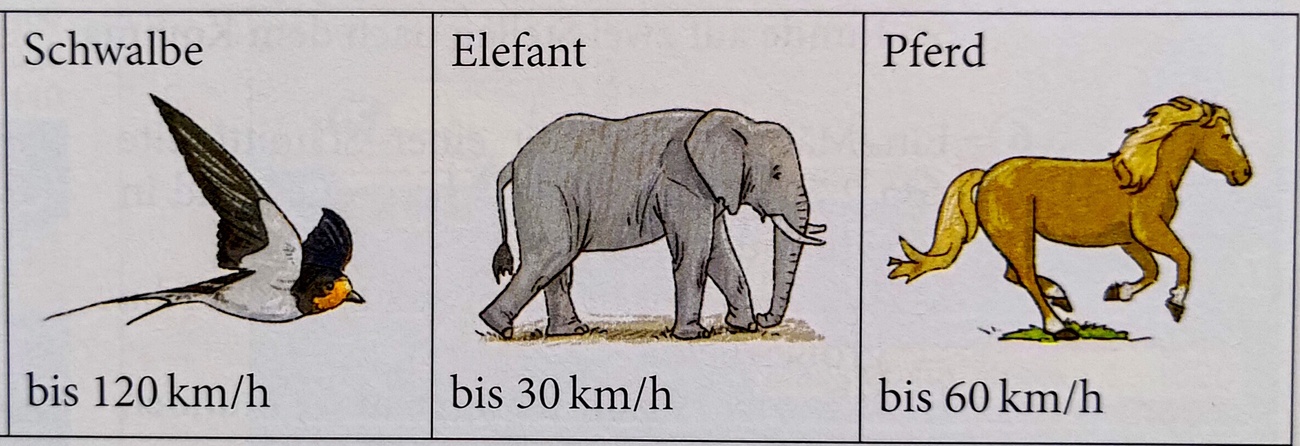
Berechne wie viele Sekunden das Pferd mit der angegebenen Geschwindigkeit für 400m braucht
|
24s
|
|
|
×
|
Berechne wie viele Sekunden die Schwalbe mit der angegebenen Geschwindigkeit für 400m braucht
|
12s
|
|
|
|
Berechne wie viele Sekunden der Elefant mit der angegebenen Geschwindigkeit für 400m braucht
|
48s
|
|
|
|
|
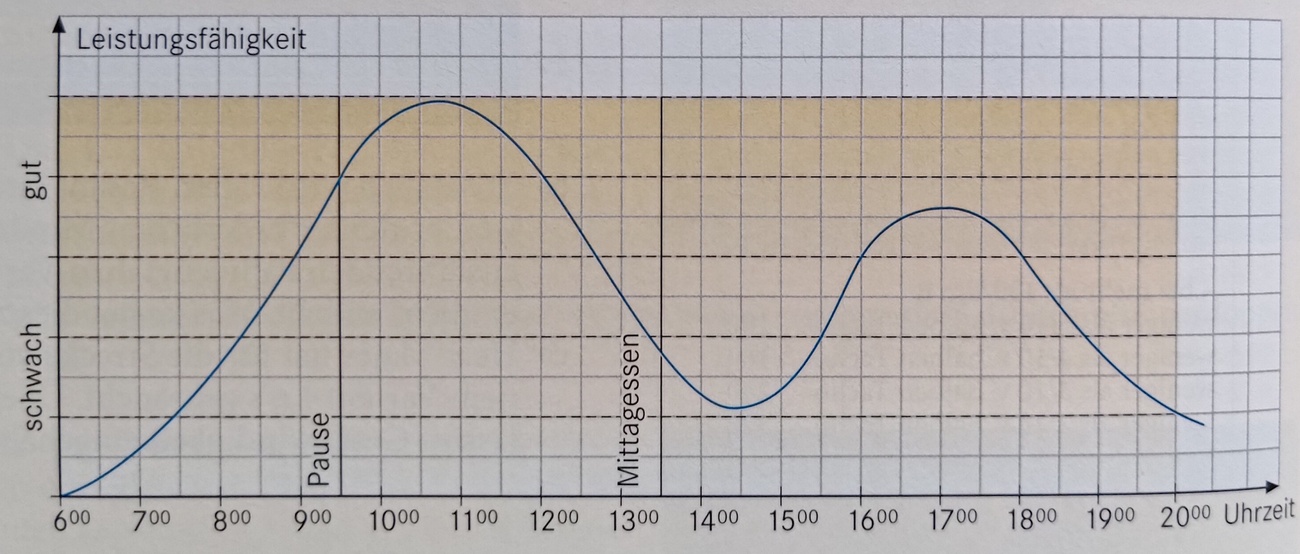
Die folgende Grafik zeigt die Leistungsfähigkeit eines Schülers an einem Schultag, der seinen täglichen Energiebedarf auf fünf Mahlzeiten verteilt hat. Gib ein Zeitfenster von zwei Stunden an, in denen es günstig für den Schüler wäre die Hausaufgaben anzufertigen.
|
zwischen 16 und 18 Uhr
|
|
Vormittags ist der Schüler in der Schule. Da kann er keine Hausaufgaben machen.
|
×
|
|
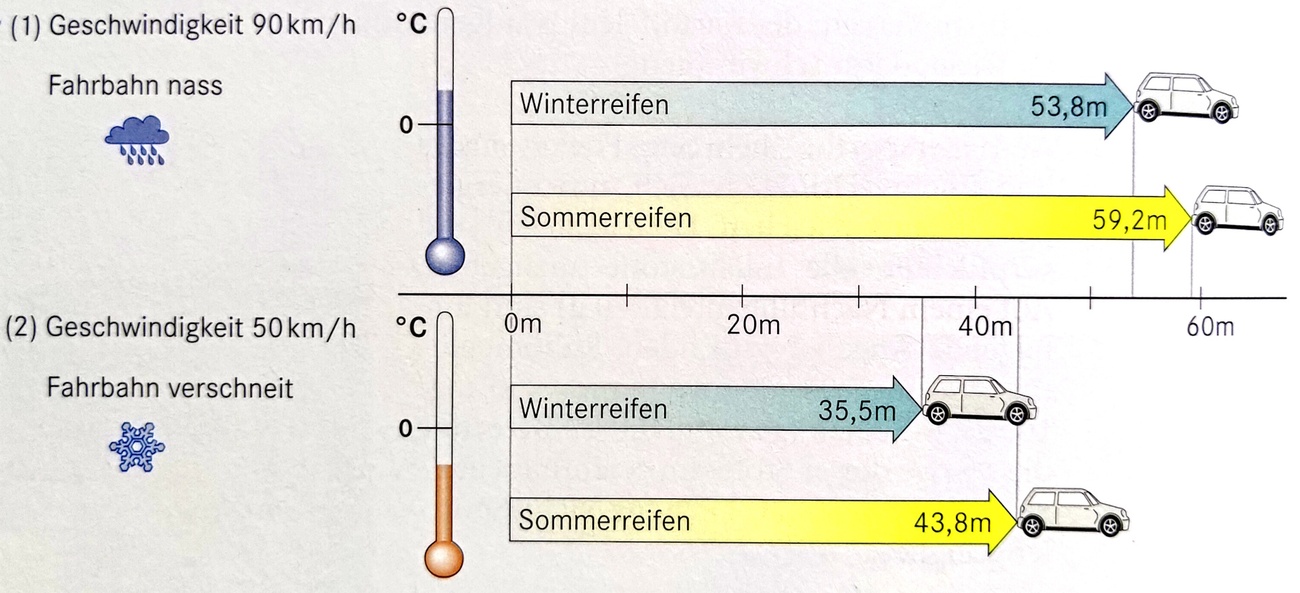
Um wie viele Meter verkürzt sich der Bremsweg durch Winterreifen bei nasser Fahrbahn laut Abbildung?
|
um 5,4m
|
|
|
×
|
Um wie viele Meter verlängert sich der Bremsweg durch Sommerreifen bei verschneiter Fahrbahn laut Abbildung?
|
um 8,3m
|
|
|
|
|
Produkte können teurer werden, ohne dass der Preis steigt. Beim genaueren Hinsehen stellt man fest, dass der Inhalt in der Verpackung bei gleichem Preis verringert wurde. Gib die Preiserhöhung in Prozent für das Knäckebrot an.
|
37,5%
|
|
|
×

|
Produkte können teurer werden, ohne dass der Preis steigt. Beim genaueren Hinsehen stellt man fest, dass der Inhalt in der Verpackung bei gleichem Preis verringert wurde. Gib die Preiserhöhung in Prozent für den Hundesnack an.
|
15%
|
|
|
|
Produkte können teurer werden, ohne dass der Preis steigt. Beim genaueren Hinsehen stellt man fest, dass der Inhalt in der Verpackung bei gleichem Preis verringert wurde. Gib die Preiserhöhung in Prozent für den Schokoriegel an (auf eine Nachkommastelle gerundet).
|
18,2%
|
|
schwierige Rechnung, weil periodische Nachkommastellen
|
|
|
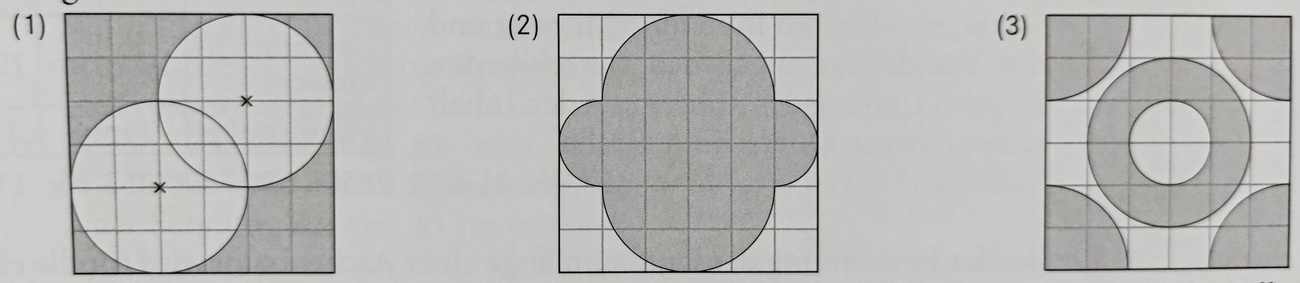
Bestimme den Flächeninhalt der grauen Fläche in Abbildung (1). Benutze dabei die Kreiszahl Π als Variable, nicht als Zahl. Ein Kästchen ist eine Einheit.
|
2*((16-4Π)*3/4)+8 = 24-6Π+8 = 32-6Π
|
|
extra schwer
|
×
|
Bestimme den Flächeninhalt der grauen Fläche in Abbildung (2). Benutze dabei die Kreiszahl Π als Variable, nicht als Zahl. Ein Kästchen ist eine Einheit.
|
Π+4Π+8 = 5Π+8
|
|
|
|
Bestimme den Flächeninhalt der grauen Fläche in Abbildung (3). Benutze dabei die Kreiszahl Π als Variable, nicht als Zahl. Ein Kästchen ist eine Einheit.
|
4Π+4Π-Π = 7Π
|
|
|
|
|
Berechne die Länge der roten Linie. Benutze dabei die Kreiszahl Π als Variable, nicht als Zahl.
|
8Π
|
|
|
×

|
|
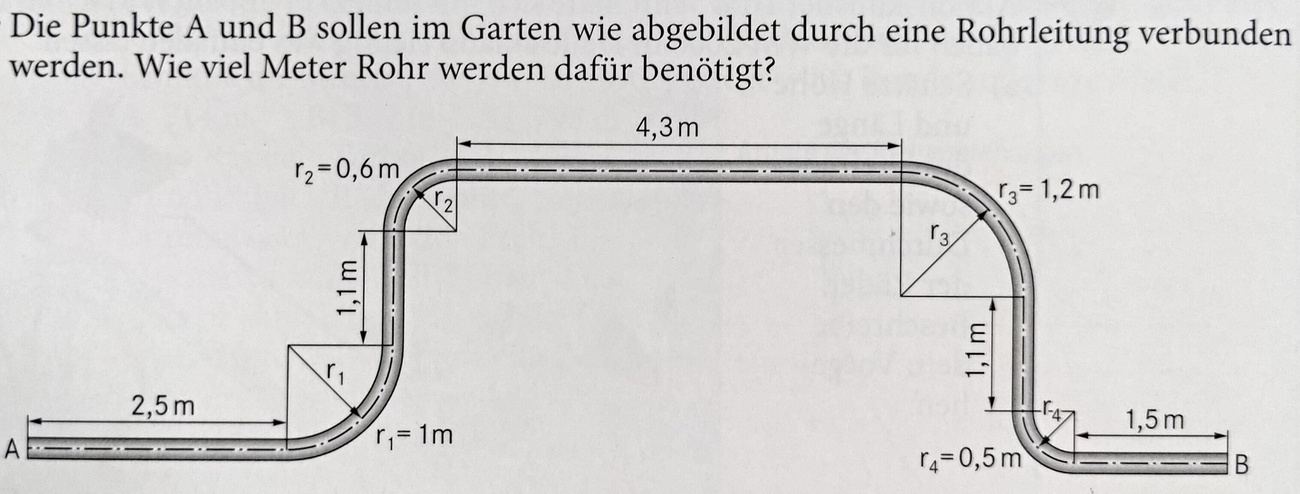
Die Punkte A und B sollen im Garten wie abgebildet durch eine Rohrleitung verbunden werden. Wie viel Meter Rohr werden dafür benötigt? Rechne zuerst den Term mit Π als Variable aus und bestimme dann die Meter mit Π=3,1. Runde das Ergebnis auf eine Nachkommastelle.
|
2,5+1,1+4,3+1,1+1,5+0,5Π+0,3Π+0,6Π+0,25Π = 7,5+1,65Π = 12,6m
|
|
Die Multiplikation ist etwas schwierig für das VLM
|
×
|
|
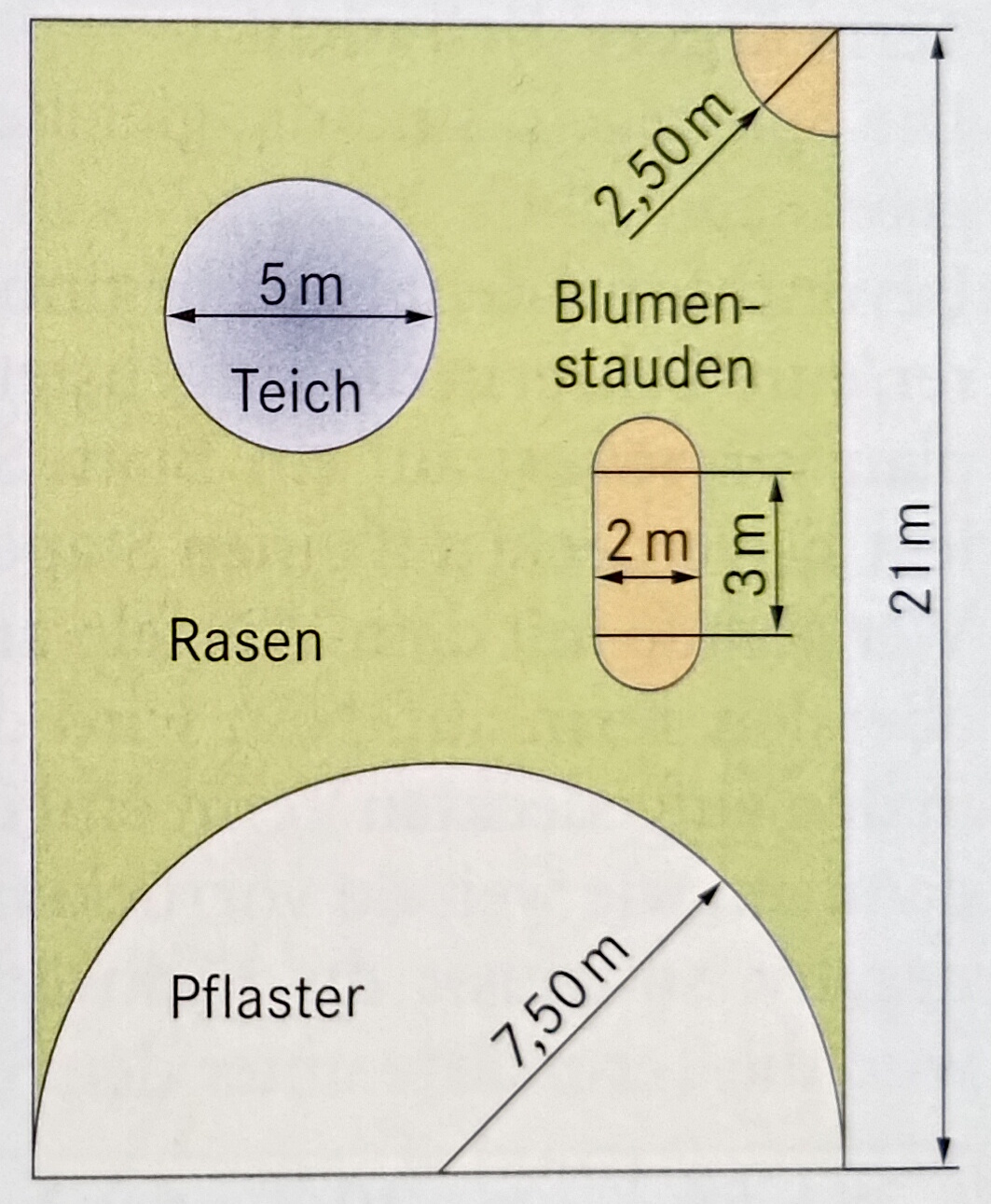
Die Abbildung zeigt einen Garten mit verschiedenen Bestandteilen. Wie groß ist er insgesamt?
|
15*21 = 315qm
|
|
|
×
|
Die Abbildung zeigt einen Garten mit verschiedenen Bestandteilen. Wie viel Platz belegt der Teich? Rechne mit Π=3,1 und runde auf eine Nachkommastelle.
|
2,5*2,5*Π = 6,25*3,1 = 19,4qm
|
|
|
|
Die Abbildung zeigt einen Garten mit verschiedenen Bestandteilen. Wie viel Platz belegen die Blumenbeete? Rechne mit Π=3,1 und runde auf eine Nachkommastelle.
|
1,5*1,5*Π+(2,5*2,5*Π)/4+2*2= 2,25Π+6,25/4Π+4 = 3,8Π+4 = 11,8+4=15,8qm
|
|
|
|
|
Welcher Boxplot gehört zu Stefan? Antworte mit dem Buchstaben
|
D
|
|
|
×

|
Welcher Boxplot gehört zu Jenny? Antworte mit dem Buchstaben
|
C
|
|
|
|
|
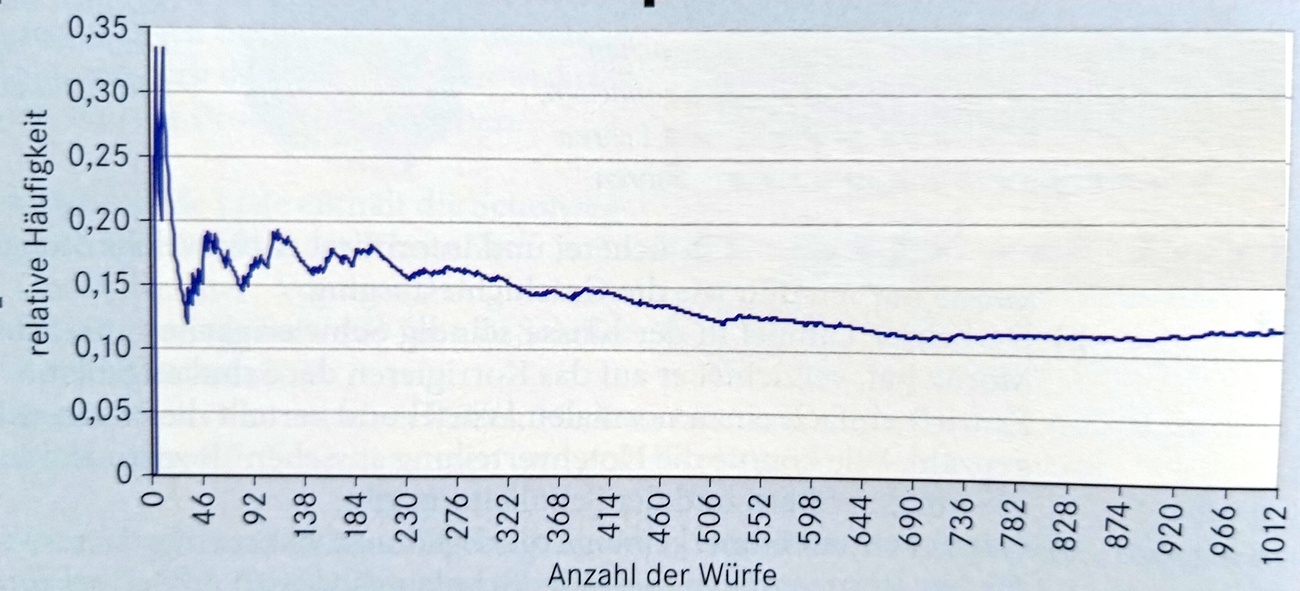
Das Diagramm zeigt die Ergebnisse von Würfelwürfen und die relative Häufigkeit der Zahl sechs. War der verwendete Würfel ein Laplace Würfel oder war er gezinkt? Begründe!
|
Der Würfel war gezinkt. Statistisch müsste die 6 mit 1/6 Wahrscheinlichkeit (16,6%) auftreten. Im Diagramm liegt sie aber deutlich unter 15%.
|
|
|
×
|
|
Mit beiden Würfeln wird je einmal gewürfelt. Berechne die Wahrscheinlichkeit, dass die gewürfelte Zahl genau fünf ist. Gib das Ergebnis als Bruch an.
|
für den sechs-seitigen Würfel ist die Wahrscheinlichkeit 1/6, für den 18-seitigen Würfel 1/18.
|
|
|
×

|
Mit beiden Würfeln wird je einmal gewürfelt. Berechne die Wahrscheinlichkeit, dass die gewürfelte Zahl größer als vier ist. Gib das Ergebnis als Bruch an.
|
für den sechs-seitigen Würfel ist die Wahrscheinlichkeit 1/3, für den 18-seitigen Würfel 7/9.
|
|
|
|
Mit beiden Würfeln wird je einmal gewürfelt. Berechne die Wahrscheinlichkeit, dass die gewürfelte Zahl kleiner als sieben ist. Gib das Ergebnis als Bruch an.
|
für den sechs-seitigen Würfel ist die Wahrscheinlichkeit 1, für den 18-seitigen Würfel 1/3.
|
|
|
|
|
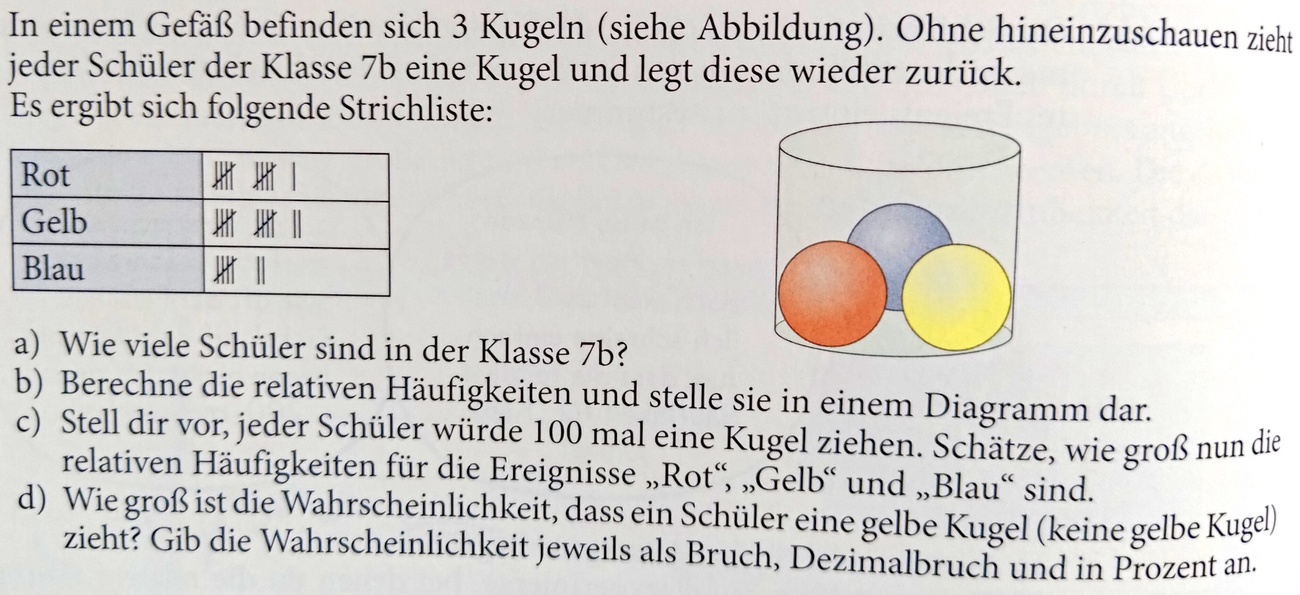
Beantworte die Frage aus Teilaufgabe a)
|
30 Schüler
|
|
|
×
|
Gib die relativen Häufigkeiten für die rote, blaue und gelbe Kugel als Bruch an.
|
rot: 11/30, gelb: 12/30, blau: 7/30
|
|
|
|
Beantworte die Frage aus Teilaufgabe c). Gib das Ergebnis in Prozent mit einer Nachkommastelle an!
|
jeweils 33,3%
|
|
|
|
|
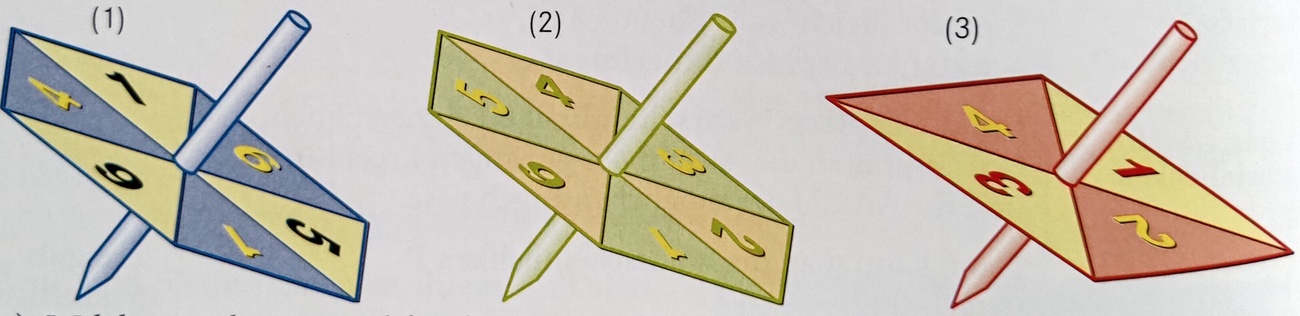
Im Bild siehst du drei Kreisel. Wie hoch ist die Wahrscheinlichkeit, mit Kreisel (1) eine sechs zu drehen? Es zählt die Zahl in dem Dreieck, an dessen Kante der Kreisel liegenbleibt.
|
ein Drittel, 33,3%
|
|
|
×
|
Im Bild siehst du drei Kreisel. Wie hoch ist die Wahrscheinlichkeit, mit Kreisel (2) eine sechs zu drehen? Es zählt die Zahl in dem Dreieck, an dessen Kante der Kreisel liegenbleibt.
|
ein Sechstel, 16,6%
|
|
|
|
Im Bild siehst du drei Kreisel. Wie hoch ist die Wahrscheinlichkeit, mit Kreisel (3) eine sechs zu drehen? Es zählt die Zahl in dem Dreieck, an dessen Kante der Kreisel liegenbleibt.
|
Es gibt keine sechs.
|
|
|
|
|
Welche Wahrscheinlichkeit für das Halten des Elfmeters wird Stefan in Teilaufgabe a) berechnen?
|
ein Viertel
|
|
|
×

|
Welche Wahrscheinlichkeit für das Halten des Elfmeters wird Leonie in Teilaufgabe a) berechnen?
|
ein Fünftel
|
|
|
|
Beantworte die Frage aus Teilaufgabe c). Gib die finale Antwort in Form eines Buchstaben
|
B
|
|
|
|
|
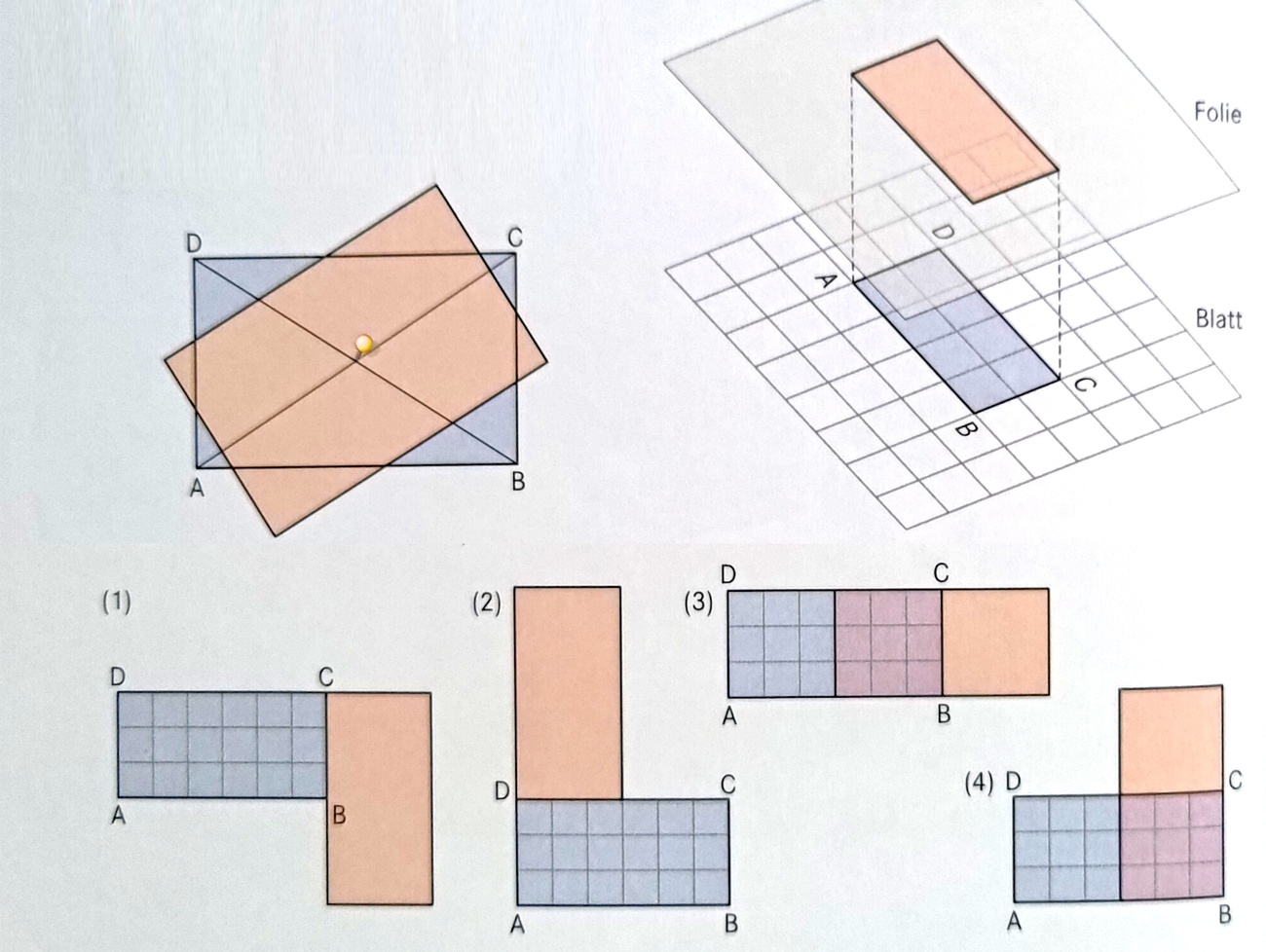
Ein rotes Rechteck auf einer transparenten Folie wird über ein Blatt mit einem identischen blauen Rechteck gelegt wie oben zu sehen. Anschließend wird eine Nadel durch Folie und Papier gesteckt, so dass sich das rote Rechteck um den Einstichpunkt drehen kann. Die Nadel kann an beliebigen Stellen eingestochen werden. Gib für die Figur (1) an, wo die Nadel eingestochen wurde, und um wie viel Grad gedreht wurde.
|
Drehpunkt C, Rotation um 90°
|
|
|
×
|
Ein rotes Rechteck auf einer transparenten Folie wird über ein Blatt mit einem identischen blauen Rechteck gelegt wie oben zu sehen. Anschließend wird eine Nadel durch Folie und Papier gesteckt, so dass sich das rote Rechteck um den Einstichpunkt drehen kann. Die Nadel kann an beliebigen Stellen eingestochen werden. Gib für die Figur (2) an, wo die Nadel eingestochen wurde, und um wie viel Grad gedreht wurde.
|
Drehpunkt D, Rotation um 90°
|
|
|
|
Ein rotes Rechteck auf einer transparenten Folie wird über ein Blatt mit einem identischen blauen Rechteck gelegt wie oben zu sehen. Anschließend wird eine Nadel durch Folie und Papier gesteckt, so dass sich das rote Rechteck um den Einstichpunkt drehen kann. Die Nadel kann an beliebigen Stellen eingestochen werden. Gib für die Figur (3) an, wo die Nadel eingestochen wurde, und um wie viel Grad gedreht wurde.
|
Drehpunkt ist der Schnittpunkt der Diagonalen des überlappenden Quadrats. Rotation um 180°
|
|
|
|
Ein rotes Rechteck auf einer transparenten Folie wird über ein Blatt mit einem identischen blauen Rechteck gelegt wie oben zu sehen. Anschließend wird eine Nadel durch Folie und Papier gesteckt, so dass sich das rote Rechteck um den Einstichpunkt drehen kann. Die Nadel kann an beliebigen Stellen eingestochen werden. Gib für die Figur (4) an, wo die Nadel eingestochen wurde, und um wie viel Grad gedreht wurde.
|
Drehpunkt ist der Schnittpunkt der Diagonalen des überlappenden Quadrats. Rotation um -90°, bzw. 270°
|
|
|
|
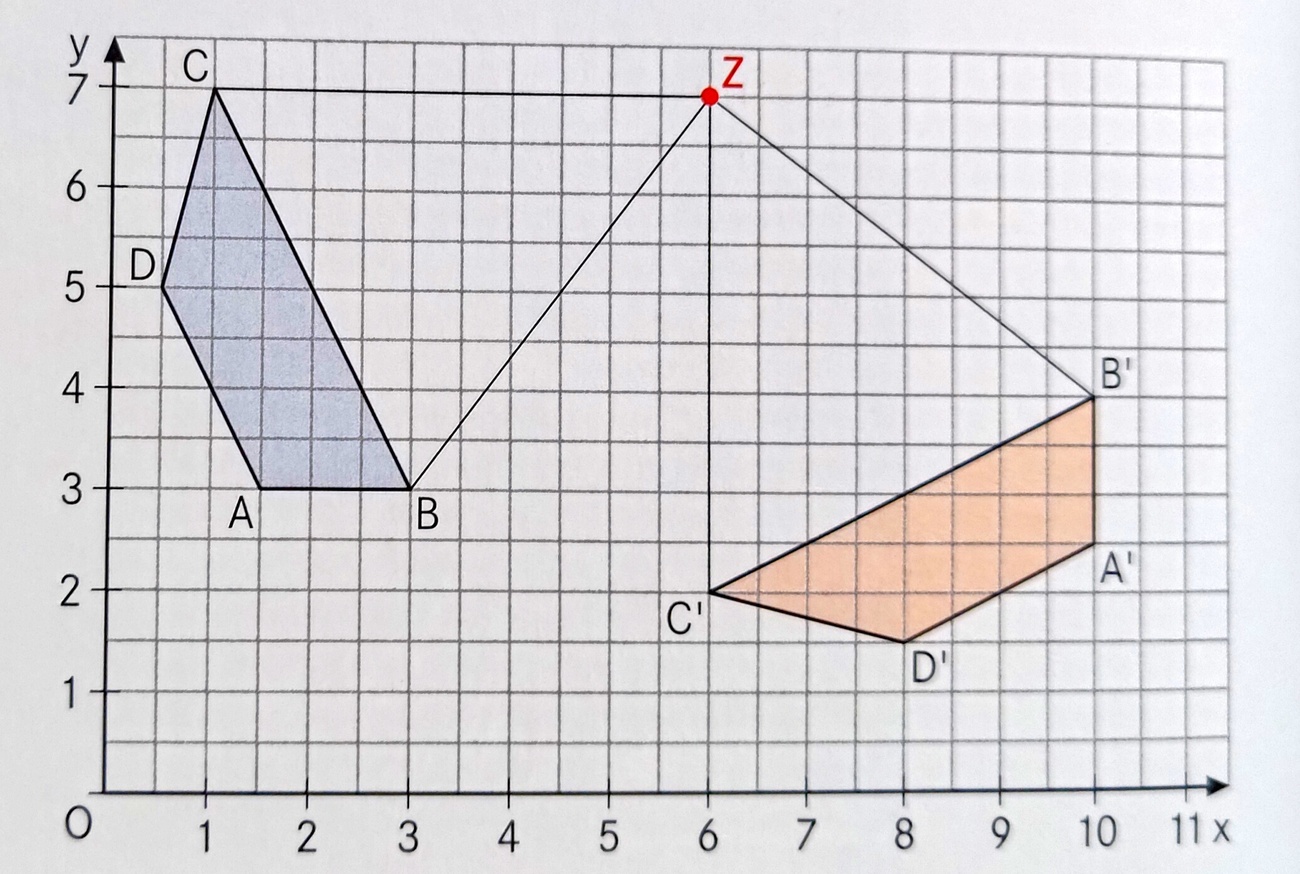
Um wie viel Grad hat sich die abgebildete Schiffsschaukel um den Drehpunkt Z gedreht?
|
90°
|
|
|
|
|
Das Rechteck ABCD wird um -90° um Drehpunkt B gedreht. Gib die Koordinaten des Punktes C' an, der durch diese Abbildung aus C entsteht!
|
C'=(6;3)
|
|
|
×
|
Das Rechteck ABCD wird um 90° um Drehpunkt A gedreht. Gib die Koordinaten des Punktes D' an, der durch diese Abbildung aus D entsteht!
|
D'=(1;0,5)
|
|
|
|
|
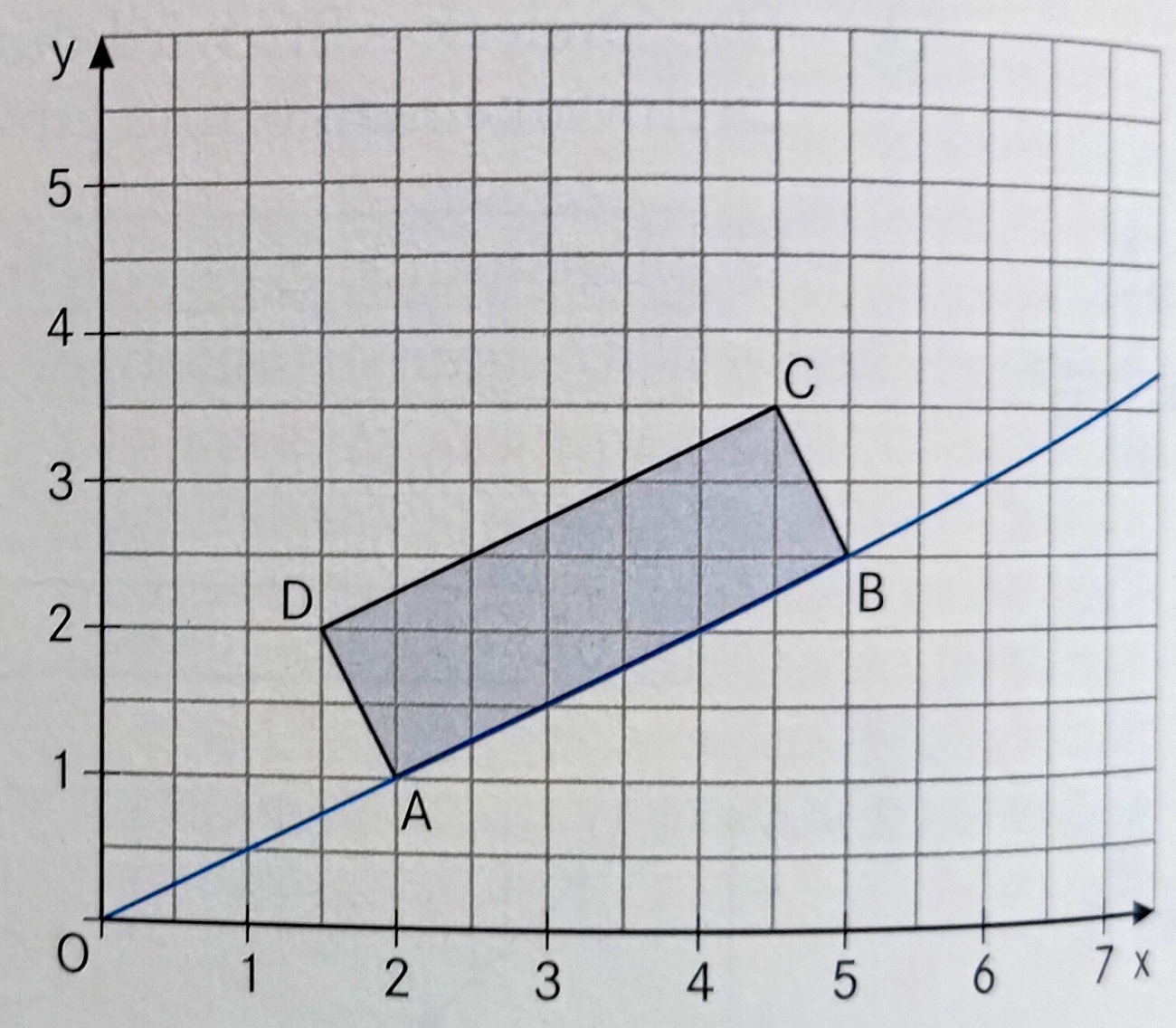
Berechne das Maß für den Winkel α
|
α=30°
|
|
|
×
|
|
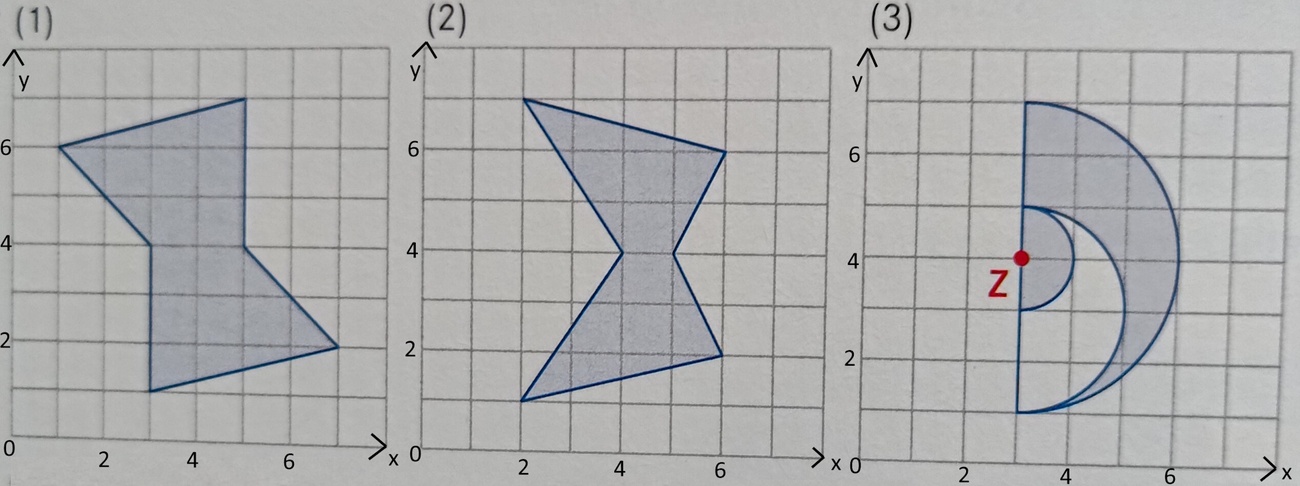
Ist eine der drei abgebildeten Figuren achsensymmetrisch? Wenn ja, dann gib die X bzw. Y-Koordinate an, durch die die Symmetrieachse läuft!
|
Figur (2) ist achsensymmetrisch. Die Symmetrieachse läuft durch y=4
|
|
|
×
|
|
Welcher der abgebildeten Kanaldeckel ist symmetrisch, wenn man die Aufschrift vernachlässigt? Gib jeweils die vorliegende Symmetrie mit an!
|
(1) ist entlang der Diagonalen symmetrisch, (2) entlang der mittleren Strebe, (3) ist symmetrisch entlang der Diagonalen, (4) ist symmetrisch entlang der Linie durch die Torhälften und das Kreuz
|
|
schlecht automatisiert zu bewerten
|
×

|
|
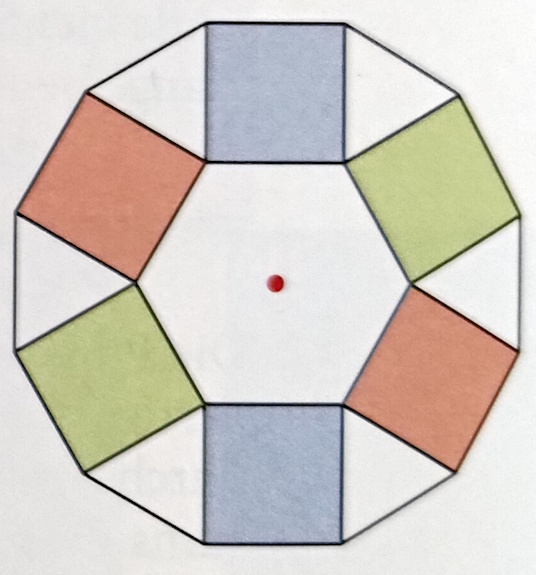
Welche Symmetrien liegen in der abgebildeten Figur vor, wenn du die Farben berücksichtigst?
|
Es gibt eine Drehsymmetrie um den roten Punkt im Zentrum.
|
|
|
×
|
Welche Symmetrien liegen in der abgebildeten Figur vor, wenn du die Farben nicht berücksichtigst?
|
Es gibt drei Symmetrieachsen, jeweils durch die Mitte der beiden gleichfarbigen Rechtecke.
|
|
|